スポンサーリンク
問題
〇、△、×のいずれかのマークが1つずつかかれたカードがあります。〇3枚、△2枚、×2枚の全7枚のカードを、同じマークのカードが隣り合わないように横一列に並べます。
一番左に○を並べた時、残りの6枚の並べ方は何通りあるか。
- 15通り
- 16通り
- 18通り
- 20通り
- 24通り
想定問題
解答と解説
解答
4
解説
樹形図で書き出していくしかありません。
左から2番目は△か×です。
△も×も残りが2個ずつであり、条件が同じです。
2番目が△のときの全並べ方がA通りあれば、
2番目が×のときの全並べ方もA通りです。
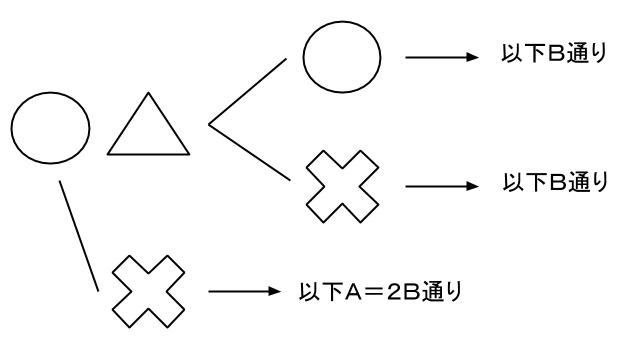
より、2番目が△のときの書き出しをします。

3番目は〇か×です。
〇も×も残り2個ずつであり、条件が同じです。
3番目が〇のときの全並べ方がB通りあれば、
3番目が×のときの全並べ方もB通りです。
より、3番目が〇のときの書き出しをします。
4番目は、×か△です。
残りは書き出します。
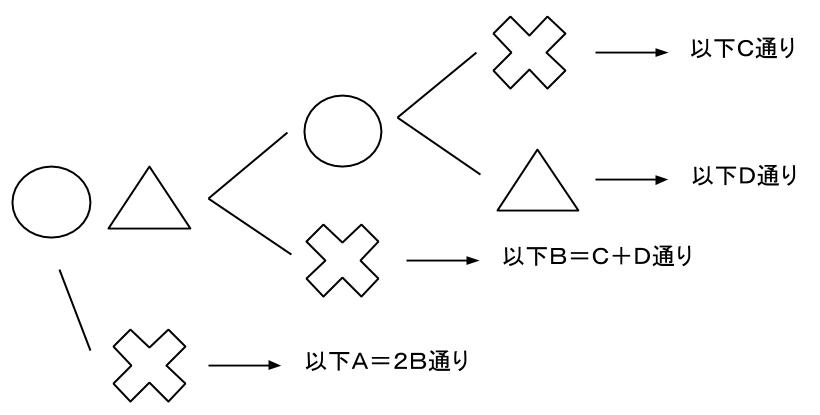
4番目が×のとき
残りは、〇×△が1枚ずつ計3枚です。
並べ方は
(〇、×、△)
(〇、△、×)
(△、〇、×)
(△、×、〇)
以上C=4通りです。
4番目が△のとき
残りは、〇1枚、×が2枚の計3枚です。
並べ方は
(×、〇、×)
以上D=1通りです。
よって、
B=4+1=5(通り)
A=2B=10(通り)
全部で、2A=20(通り)です。
スポンサーリンク
