スポンサーリンク
問題
横一列に並んでいる〇を、左から斜線で消していく。一度に消せる〇の数を1個か2個とした場合、例えば〇の数が3個並んでいるときは次のように3通りある。
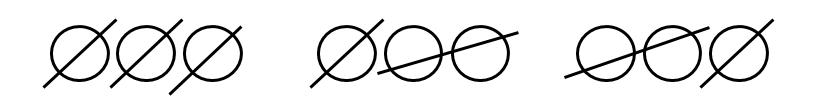
一度に何個でも〇を消してもよいとした場合、〇が6個並んでいるとき、すべての〇を消す方法は何通りあるか。
- 20通り
- 24通り
- 28通り
- 32通り
- 36通り
想定問題
解答と解説
解答
4
解説
○が階段で、消した○まで階段を上ったと見なせば、
1段上り、2段上り・・・6段上りまで可能な、全6段の階段上りと同一視できます。
| 1段 | 2段 | 3段 | 4段 | 5段 | 6段 |
| 1 | 2 | 4 | 8 | 16 | 32 |
前問までの通り、表であっさり答えがでます。 32通りです。
追加問題
上の問題の解説で規則性があることに気づきましたか。一度に何段でも上ることのできる階段上りでは、N段まで上る上り方は、2のN乗通りになっています(先の表を確認してください)。
では、どうしてそうなるのか考えてみてください。
発想の転換が必要でおもしろいですよ。
では、どうしてそうなるのか考えてみてください。
発想の転換が必要でおもしろいですよ。
解答と解説
解説
〇と〇が線でつながっているかいないか、という視点で本問を見てみましょう。
〇と〇の間は5箇所あるので、その5箇所についてそれぞれ、
繋がっている、繋がっていない の2通りの選択があります。
よって、2の5乗=32(通り)となります。
スポンサーリンク
