スポンサーリンク
問題
1~6の6個の整数から重複のないように無作為に3つの整数を選んだとき、各整数を辺の長さとする三角形ができる確率はいくらか。
- 1/5
- 1/4
- 3/10
- 7/20
- 2/5
国税 労働基準 2007
解答と解説
解答
4
解説
どのようなときに三角形ができるのか、という知識が必要です。
「最も長い辺」<「他の2辺の和」
となるときです。
下図を見れば明らかでしょう。
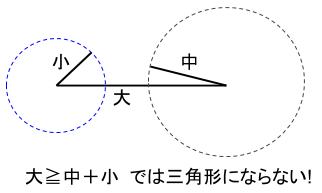
よって、三角形ができるような数の組をまず書きだします。
最も長い辺が6のとき可能なもの、5のとき可能なもの・・・と順に書き出しましょう。
(6、5、4)
(6、5、3)
(6、5、2)
(6、4、3)
(5、4、3)
(5、4、2)
(4、3、2)
以上7組となります。
また、6個の整数から無作為に3個を選ぶ組合わせは、
6C3=20(通り)
より、7/20 となります。
スポンサーリンク
