スポンサーリンク
問題
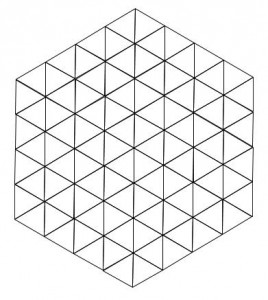
下の図は1辺が4cmの正六角形を、1辺が1㎝の正三角形に分割したものです。この図の中に正六角形は全部で何個ありますか。
- 60通り
- 64通り
- 68通り
- 72通り
- 76通り
想定問題
解答
解説
まずは真っ当に解いてみましょう。
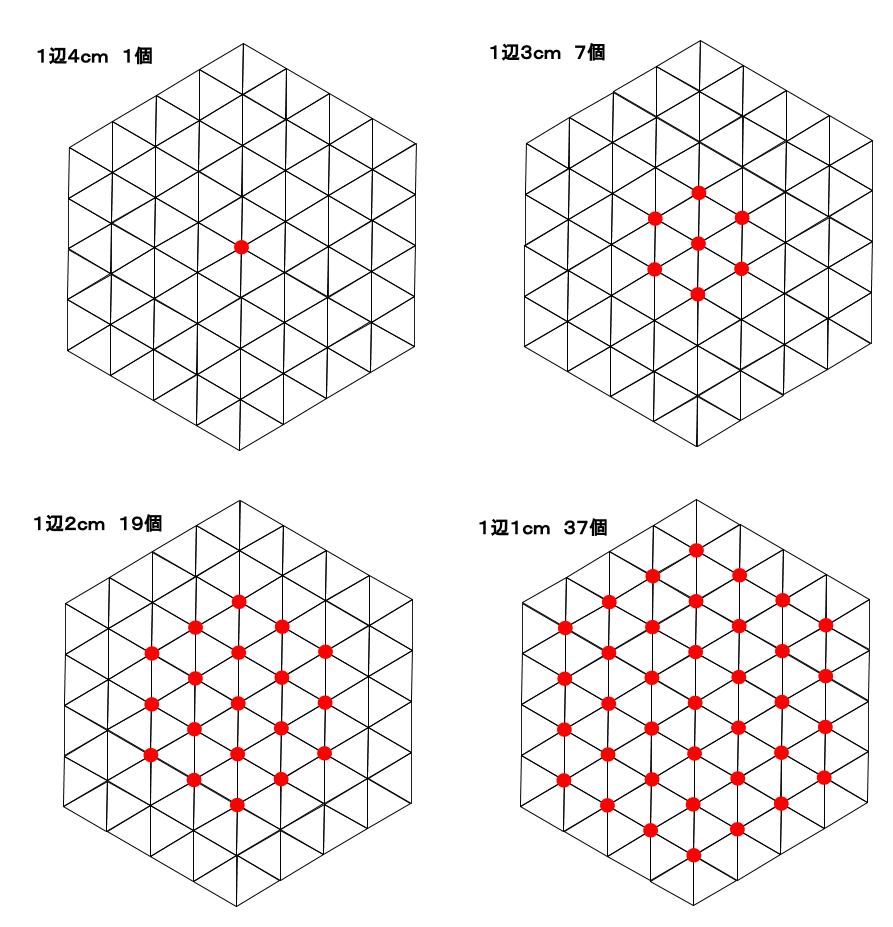
例えば、1辺が3cm の正六角形は何個あるか数えてみます。
1つの正六角形に対して、1つ中心点が対応するので、中心点に着目した方がすっきり数えられます。
7個ありますね。
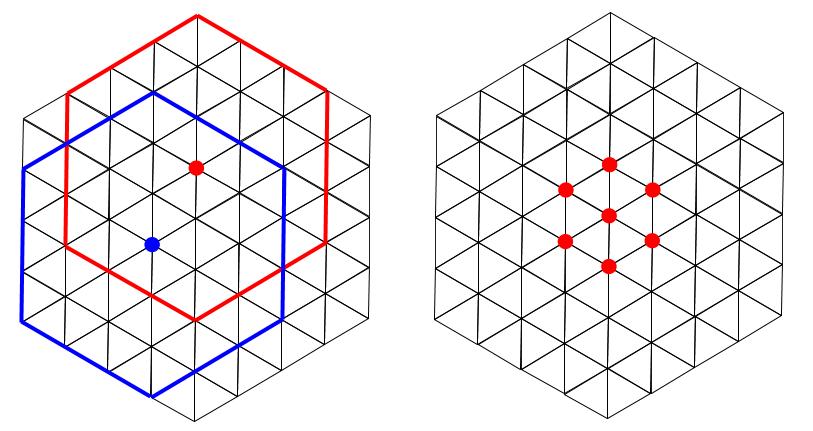
同様に、1辺が4cmの正六角形、1辺が2cmの正六角形、1辺が1cmの正六角形も数えます。
以上より、1+7+19+37=64(個)が求める答えとなります。
1辺の2cmの正六角形が19個、1辺の1cmの正六角形が37個、どちらも数えるのが結構たいへんですね。この解法をふまえて、衝撃的な別解を紹介します。とてもおもしろい知的興奮が味わえると思います。
別解
本問は定番問題ですが、以下の衝撃的な別解はあまり知られていないようです。
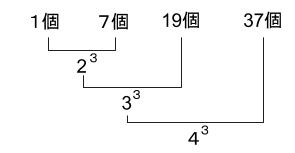
枠の正六角形の1辺が4cmのときに、答えが、64=4の3乗 となったわけですが、
もしかして・・・・
1辺がNcmのときに、答えが、Nの3乗 となるのではないか
と予想されます。
実際にこの予想が成り立ちそうであることは、すぐに調べられますが、
では、なぜ成り立つのか。なぜ3乗になるのか。
腕に覚えのある方はぜひ考えてみてください。
以下、衝撃的な別解を紹介します。
3乗なので、何やら立方体と関連付られそうな予感がしませんか。
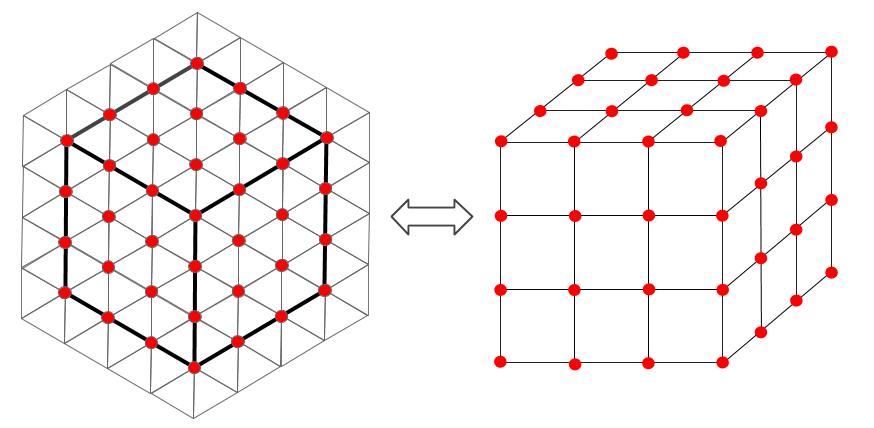
改めて下図をよく見てください。立方体に見えてきませんか?
左図の赤丸の数は、4×4×4=64(個)のうちの見えている部分とみなせます。見えていない部分は、3×3×3=27(個)の立方体なので、64-27=37(個)となります。実際に数えた値と一致しますね。
これが、1+7+19+37=64=4の3乗 となった理由です。
スポンサーリンク