スポンサーリンク
問題
下図のように円周を12等分する点があり、それらの点から3個を選び、直線で結んで三角形をつくります。全部で何種類の三角形ができますか。ただし、裏返したり回転させて重なるものは一つとします。下図の2つの三角形は同じ三角形です。
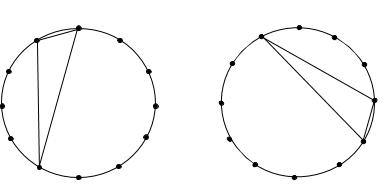
- 12種類
- 14種類
- 16種類
- 18種類
- 20種類
想定問題
解答と解説
解答
1
解説
まずは様々に図示をしてみましょう。回転、裏返しで同じものは排除するので結構厄介です。本質的な仕組みを見抜いてください。
さて、三角形の形は何で決まりますか。選んだ点と点の間がどれくらい離れているかで辺の長さが決まります。この辺が3つで三角形の形が決まるわけですから、「点と点の間がどれくらい離れているか」に着目すれば解決します。
問題中にある三角形は(1,4,7)と表せます。
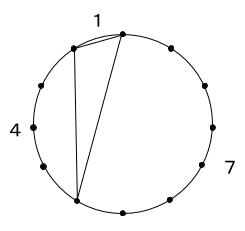
結局、12を3つの正の整数に分解するやり方の総数を求めればよいです。ここから先は書き出しです。
(10、1、1)
(9、2、1)
(8、3、1)
(8、2、2)
(7、4、1)
(7、3、2)
(6、5、1)
(6、4、2)
(6、3、3)
(5、5、2)
(5、4、3)
(4、4、4) 12種類です。
スポンサーリンク
