スポンサーリンク
問題
A 組、B 組、C 組、D 組、E 組、F 組の人数はすべて異なります。クラスの人数を少ない順にならべたところ、連続した6つの整数となり、最も人数が少ないのはC 組でした。また、A 組とB 組の人数の和、C 組とF 組の人数の和、D 組とE 組の人数の和はすべて等しく、A 組とD 組の人数の和よりB 組とE 組の人数の和のほうが多く、A 組とF 組の人数の和はD 組の人数の2倍に等しくなりました。このとき、次の5つの選択肢の中から正しいものを選べ。
- A 組の人数はE 組の人数より多い
- B 組の人数はD 組の人数より多い
- 人数が少ない方から3番目の組はB 組である
- B 組の人数とE 組の人数の差は1人だ
- A 組の人数とE 組の人数の差は2人だ
想定問題
解答と解説
解答
2
解説
C 組の人数をX人とします。最も人数の多いクラスがF。
AとBの組、あるいはDとEの組は下図のオレンジか青のいずれかです。

「A 組とF 組の人数の和はD 組の人数の2倍」という情報は、
「A 組とF 組の人数の平均はD 組の人数と等しい」 と言い換えられます。
これにより、AとDの入る場所の候補は2パターンになり、自動的に残りのBとEもきまります。
パターン1
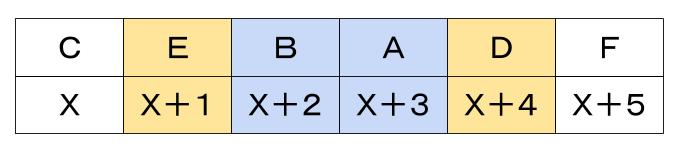
パターン2
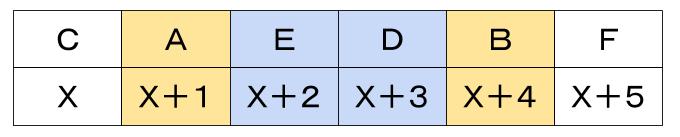
さらに、A 組とD 組の人数の和よりB 組とE 組の人数の和のほうが多い
を使うとパターン2の方が正しいと決まります。
これを見ながら選択肢を順に検討していきます。
選択肢2 「B 組の人数はD 組の人数より多い」 が正しいことがわかります。
スポンサーリンク
