スポンサーリンク
問題
比重0.9、1.0、1.2の溶液A、B、Cを混ぜて10mlの混合溶液を作り、重さを量ったところ、10.1gであり、BとCの溶液の量を逆に加えてしまったことに気づいた。そこで、A、B、Cをそれぞれ追加し、20mlの正しい割合の混合溶液を作り、重さを量ったところ、19.8gであった。このとき、追加した溶液Bの量は何mlか。
ただし、混合溶液の体積はそれぞれの溶液の体積の和になるものとする。
- 3.5ml
- 4.0ml
- 4.5ml
- 5.0ml
- 5.5ml
2003 国家Ⅱ種
解答と解説
解答
2
解説
はじめに作った混合溶液
溶液Aをaml、溶液Bをbml、溶液Cをcml 混ぜたとします。
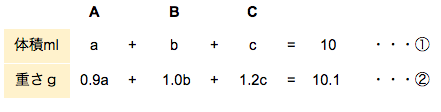
作りたかった混合溶液
最終的にできた正しい混合溶液20mlの半分の量を作りたかったので、その重さは19.8gの半分で、9.9gです。
また、溶液Bをcml、溶液Cをbml で混ぜるのが正しい混ぜ方です。
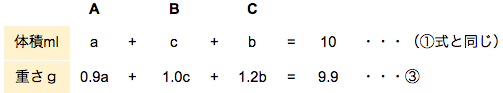
この①②③で連立方程式を解けば求まります。
a=5 b =2 c=3 です。
このことから、下のようにまとめられます。
はじめに作った混合溶液

あとに作り直した混合溶液(作りたかった混合溶液の2倍)

はじめに溶液Bは2ml使いましたが、最終的には、6ml使っています。追加した量は、4mlです。
別解(ちょっと違った視点)
上の2パターンの混合溶液、はじめに作った混合溶液と作りたかった混合溶液を混ぜると下のようになり、これは溶液Bと同じ比重です。
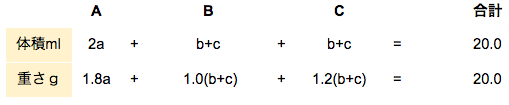
つまり、AとCを混ぜると、比重が1.0になるように混ぜています。これは、AとCを体積比2:1で混ぜていることがわかります(てんびん図などで計算できますね)。
このことから、下記のように混ぜている事がかわります。

この後、結局ははじめの解説での式、①、②、③を利用して連立方程式を解くこととなります。
この別解の視点によって、楽な解法が見つかることはありませんでしたが、それは結果論にすぎません。問題中の様々な数とその関係についてアンテナを張り巡らしておきましょう。
スポンサーリンク
