【ニュートン算基礎】

解答

解説

ニュートン算になる前のヒヨコのような問題です。
まずは本問で、ニュートン算の基礎固めをしておきましょう。

この問題は、「邪魔のある仕事算」といえます。
「水をくみ出す仕事」に対して、湧き出しという仕事の邪魔があります。
ニュートン算はこのような邪魔がある状況を整理していく問題なのです。

２つの見方を押さえておきましょう。

１．毎分に着目

毎分１１Ｌずつくみだし、ＸＬずつ湧き出すので、
１分あたり、１１－Ｘ（Ｌ）ずつ仕事が進みます。
よって、１２０÷（１１－Ｘ）＝１５
となり、Ｘ＝３（Ｌ）と求まります。

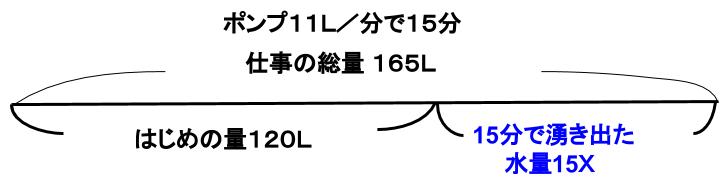
２．仕事の総量に着目

くみ出す水の総量は、はじめの１２０Ｌと１５分で湧き出た水量Ｘ×１５＝１５Ｘ（Ｌ）の和になります。
これは１１×１５＝１６５（Ｌ）なので、
１２０＋１５Ｘ＝１６５
より、Ｘ＝３（Ｌ）と求まります。

２つの解き方はどちらもまったく同じです、数学的には差はありません。
どちらの物の見方もあたりまえ、と思えるのが理想的です。

問題の状況を、線分図で整理しながら立式したい場合は、２、総量に注目の方が相性がいいといえます。
※比の処理に習熟していれば、１．で解くことで、方程式の処理よりも容易になることも多いです。

次からはいよいよニュートン算を見ていきましょう。

解答

解説

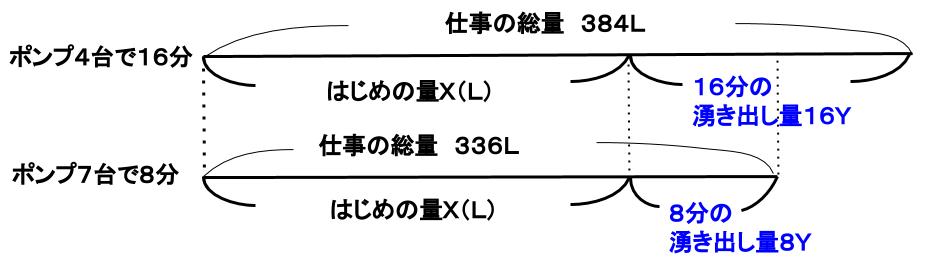
線分図に整理しながら解いてみましょう。
作業開始時の水量をＸＬ
湧き出す水量をＹＬ／分
とすると、
Ｘ＋１６Ｙ＝２４×１６・・・（４台は１分で２４Ｌくみ出す）
Ｘ＋８Ｙ＝４２×８・・・（７台は１分で４２Ｌくみ出す）

仕事の総量の差に着目します。
８Ｙ＝４８・・・（仕事の総量の差）
Ｙ＝６（Ｌ）・・・１分間の湧き出し量が求まった
よって、はじめの水量Ｘ＝288（Ｌ）が計算で求まる。
ポンプ３台で仕事をすると、
288÷（６×３－６）＝２４（分）　より24分と求まる。

基礎編はあともう１問です。具体値がまったくない問題で、ここまで深化したものをニュートン算とよぶのが本筋です。
しかし問題のカテゴライズがどうであるか、という話題はどうでもいいことですね。

解答

解説

作業開始時の草量をＸ
１日に伸びる（増える）草量をＹ
牛１頭が１日に食べる草の量をＺ
とすると、
Ｘ＋３６Ｙ＝４Ｚ×３６・・・（４頭で36日）
Ｘ＋２８Ｙ＝５Ｚ×２８・・・（５頭で28日）

あれ？未知数が３つなのに、式が２つしかつくれない・・・
ニュートン算が苦手な人の多くは、ここからどうしたらよいか迷ってしまうのですね。

結論をいうと、２つの式があるので、２つの文字が消せます。
だから、すべてＸ（ＹでもＺでもよい）だけで表せます。
つまり、
作業開始時の草量も、
１日に伸びる（増える）草量も
牛１頭が食べる草の量も
すべてＸだけで表現できるのです。
つまり、３量の比がわかるのです。
だから、最後に聞かれていることも計算して求められます。
この計算処理を楽勝で行える人はそれでＯＫです。

この最後の計算処理が不安な人には、
線分図を利用した解法をおススメしたいと思います。
改めて最初から解きなおすので、そのつもりで読んでください。

牛１頭が食べる草の量をＸとします。
※これ以上未知数はおきません！！

牛が食べた草の総量が違うのはなぜか。
８日分、多く伸びた草の量です。
だから、８日で伸びた草＝４Ｘ
つまり、１日に伸びる草の量＝0.5Ｘ　です。

これを用いれば、はじめの草の量も計算できます。
※線分図で視覚化しているため、何をどうやって計算すればよいか、迷いませんね！
144Ｘ－３６×０．５Ｘ＝126Ｘ・・・はじめの草の量
よって、11頭放牧すると
１２６Ｘ÷（１１Ｘ－０．５Ｘ）＝１２（日）　12日と求まりました。