スポンサーリンク
問題
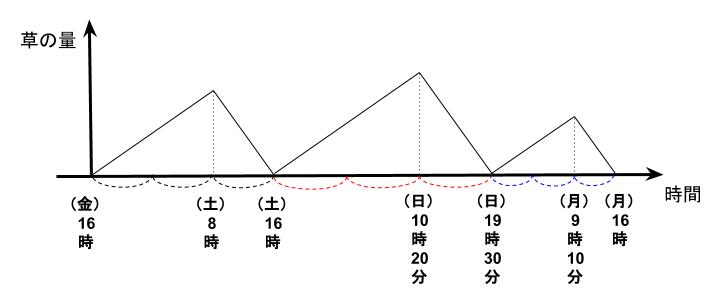
ある公園では、昼も夜も常に一定の割合で伸びている草を、午前中のうちに刈り始めて、ちょうど草がなくなったときに刈り終えることにしています。毎日午前8時に刈り始めて、ちょうど午後4時に刈り終える、ということを繰り返していましたが、ある日曜日の朝、都合で草刈りを始める時刻が遅れてしまい、午前10時20分に草刈りを始めました。翌日の月曜日の朝も、草刈りを始める時刻は午前8時より遅くなりましたが、この日はいつも通りちょうど午後4時に刈り終えることができました。月曜日は何時から草刈りを始めましたか。
- 午前8時40分
- 午前8時45分
- 午前9時00分
- 午前9時10分
- 午前9時15分
想定問題
解答
解説
状況を把握することが全てです。パターン暗記では太刀打ちできない良問です。
午後4時から、翌日の午前8時まで16時間あります。この16時間で伸びた草を、毎日
午前8時から、午後4時までの8時間で刈り終えます。
1時間で伸びる草の量を \(x\) とすると、
\(16x÷(人の作業量-x)=8\)
人が1時間で刈る作業量は \(3x\) であることがわかります。
日曜日は午前10時20分に刈り始めたので、スタート時にある草の量は、
土曜の午後4時からの18時間20分 (\(18\)\(\frac{1}{3}\)時間)で伸びた草の量なので \(18\)\(\frac{1}{3}\)\(x\)
この量を刈り終えるためにかかる時間は
\(18\)\(\frac{1}{3}\)\(x÷(3x-x)=\)\(9\)\(\frac{1}{6}\)(時間)=9時間10分
よって、この日の作業終了時刻は午前10時20分の9時間10分後である、午後7時30分です。
月曜日は、仕事のスタート時刻が分からないので全仕事量に着目します。
前日の午後7時30分から、月曜日の午後4時まで、20時間30分あるので、
この間に伸びた草の量は、\(20.5x\) です。この量を人が作業するのに、
\(20.5x÷3x=6\)\(\frac{5}{6}\)時間 =6時間50分 かかるので、
作業終了時刻である午後4時の6時間50分前が、作業開始時刻で午前9時10分です。
別解
本問は \(x\)/時ずつ伸びる と \(2x\)/時ずつ減る の繰り返し と見抜ければ以下のようにまとめられます。
スポンサーリンク
→ ニュートン算 問題1 → 仕事算とニュートン算 問題一覧
