【約数・倍数・素因数分解】基礎②

解答

解説

（１）あまり共通タイプ

5で割っても6割っても１余る数とは
５の倍数＋１　かつ　６の倍数＋１
を満たす数でこれはもちろん
５と６の公倍数＋１
となる数です。これは５と６の最小公倍数３０を用いて
３０の倍数＋１
と表せます。
200に最も近いのは、
３０×６＋１＝１８１
３０×７＋１＝２１１
のうち、２１１の方です。

（２）不足共通タイプ

あまり共通でないとき、不足共通かどうかをチェックします。
5で割ると１余る数とは、５の倍数－４と言い換えられます。
同様に
７で割ると３余る数とは、７の倍数－４と言い換えられます。
どちらも４不足していて、不足共通タイプです。
上の２つを両方満たす数とは、５と７の最小公倍数３５を用いて
３５の倍数－４
と表せます。
400に最も近いのは、
３５×１２－４＝４１６　です。

（３）共通なしタイプ

あまりも不足も共通でないときは、書き出しで調べます。
〇８で割って１余る数
１、９、１７、２５、３３、・・・

〇７で割って４余る数
４、１１、１８、２５、・・・

いずれの数列にも出現する数、
今回は２５がみつかりました。
８で割って１余り、７で割って４余る最小の数は２５です。

書き出しは１つ見つかればＯＫです。
次にいずれの数列にも出現する数をＡとすると
Ａ＝２５＋８の倍数　かつ　２５＋７の倍数
なので、
Ａ＝２５＋５６の倍数
と表せます。

よって、２５、８１、１３７、１９３、２４９、３０５・・・となるので
２５から２４９までの5個となります。

参考
条件に合う数は、Ｐ＋５６の倍数（Ｐは56未満の数）となるので、
３００÷５６＝５あまり２０
より、5個か4個のいずれかである。

（４）複合タイプ

３つすべてあまり共通、あるいは３つすべて不足共通なら、
（１）や（２）の解法でズバッと解きましょう。
今回は、
３で割って１余り、７で割って５余る
の２つが、不足共通です。
まずはこの２つを満たす数を求めます。
（２）と同様に考えて、３で割って１余り、７で割って５余る数は
２１の倍数－２
と表せます。

つまり、２１の倍数－２を満たす数の中から、５で割って２余る数を探します。
余りも不足も共通はないので、（３）のように書き出しで探します。

２１の倍数－２は以下のようになります。
１９、４０、６１、８２、・・・
順に５で割って２余るかどうかを調べます。
８２が見つかります。

３で割って１あまり、５で割って２余り、７で割って５余る最小の数は、８２です。

以下、３と５と７の最小公倍数１０５足すごとに条件を満たす数はでてくるので、
2番目に小さい数は
８２＋１０５＝１８７
です。

解答

解説

積を分解していますので、素因数分解がカギになります。
１５８４を素因数分解しましょう。

解答

解説

約数の個数は素因数分解から得られます。

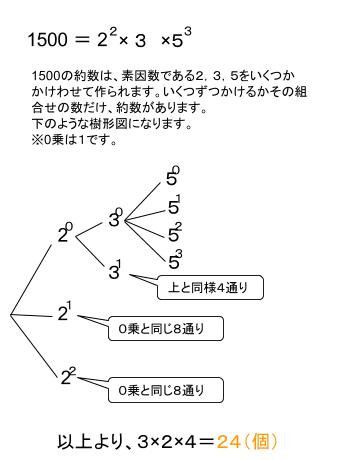
この考え方を利用して（２）を解きましょう。