スポンサーリンク
問題3
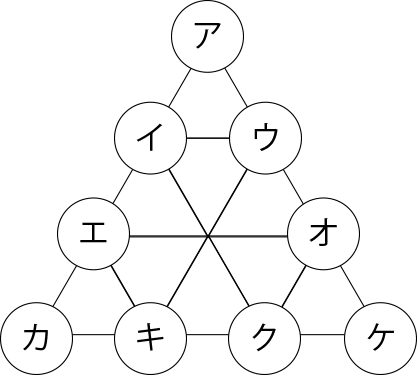
次の図で、アからケまでの9つの点を選んで、それらを頂点とする正三角形をつくれば、全部で7つできる。
いま1から9までの9個の整数を、アからケの点に1つずつ入れて、それぞれの正三角形の頂点の3つの数の和をすべて等しくしたい。このとき、ウの数を1とし、エに2、クに3を入れたとき、9の入る場所はどこか求めなさい。
- ア
- イ
- オ
- カ
- キ
想定問題
解答と解説
解答
5
解説
1から9までの9個の整数の和は45です。
下図の3つの正三角形の頂点の数の和が等しくなることから、それぞれの正三角形の頂点の3つの数の和は、45÷3=15になります。
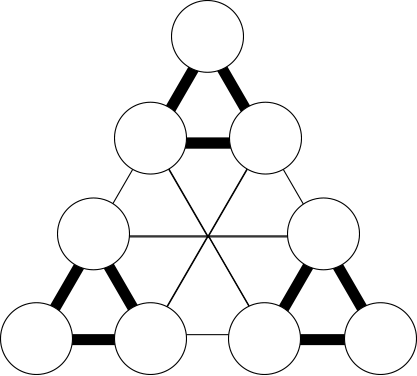
次に下図のように、オに入る数をX、ケに入る数をYとします。
右下の正三角形の頂点の和から、X+Y=12 です。
このとき、下記のようになります。
- 緑色の正三角形に着目して、キに入る数がX+2
- 青色の正三角形に着目して、アに入る数がY+1
- 赤色の正三角形に着目して、カに入る数がY-1
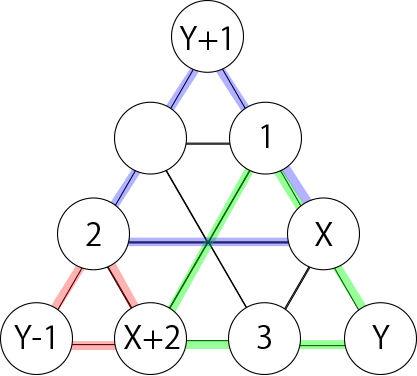
最も大きい正三角形に着目して、(Y+1)+(Y-1)+Y=15 よりY=5
よって、X=7となります。
X+2=9なので、キに9が入ります。
スポンサーリンク
