スポンサーリンク
問題
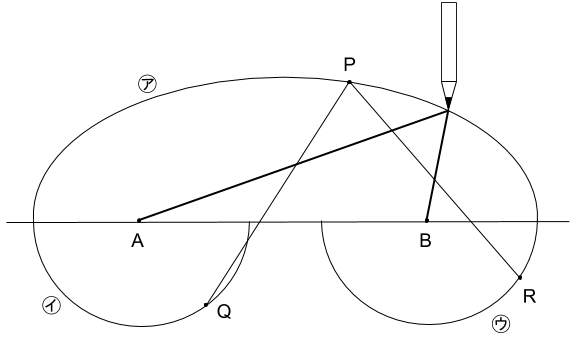
7cm離れた2点A、Bに長さ12cmの糸の両端を固定し、鉛筆でピンと張った状態で線をかいたところ、図の㋐のような曲線がかけました。さらに、図のように、2点A、Bを中心とする等しい半径の半円㋑、㋒をかきました。曲線㋐の上を点P、曲線㋑の上を点Q、曲線㋒の上を点Rが動きます。PQとPRの長さの和がもっとも大きくなったとき、その長さの和は何cmか。
- 15cm
- 16cm
- 17cm
- 18cm
- 19cm
想定問題
解答と解説
解答
3
解説
下図のように、鉛筆が曲線アの左端にある状態を考える。
12cmの糸を赤色で示しています。
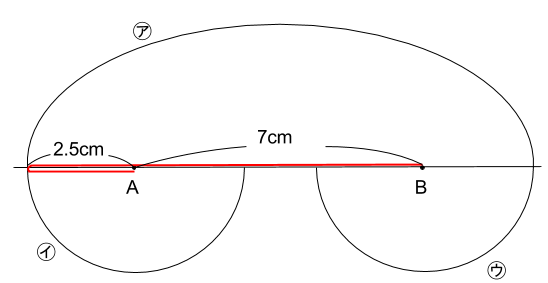
半円イの半径が、(12-7)÷2=2.5(cm)とわかります。
もちろん半円ウの半径も2.5cmです。
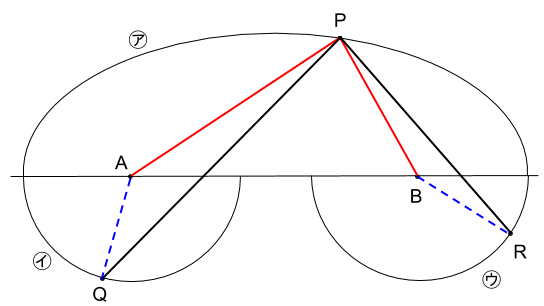
次に点P、Q、Rが下図にような位置にあるとします。
このとき三角形の3辺の長さの関係から、
PQ<PA+AQ
PR<PB+BR
となっていることが分かります(黒は、赤+青より短い)。
点Pを固定して、点Qを動かしてみれば
PA+AQの長さは、PAQが一直線上になったときに最大となります。
同様に、点Pを固定して、点Rを動かしてみれば
PB+BRの長さは、PBRが一直線上になったときに最大となります。
より、PQとPRの長さの和を最大にするためには、
PAQが一直線上かつ、PBRが一直線上になったときとわかります。
では次に点PがどこにあればPQとPRの長さの和が最大になるか考察します。
下図で考えます。
点Pを曲線ア上のどこに動かしても、PQとPRの長さの和は、青い半径2つ分と、赤い糸の長さの和であることがわかります。
つまり、点Pはどこにあっても、PQとPRの長さの和は一定です。
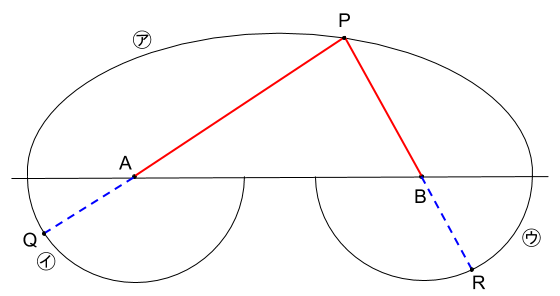
より、
PQとPRの長さの和を最大にするためには、
PAQが一直線上かつ、PBRが一直線上になったときであり、点Pはどこにあってもよい。
そしてPQとPRの長さの和の最大値は、2.5×2+12=17(cm)となります。
スポンサーリンク
