数的処理(数的推理・判断推理)が苦手である、という受験生は多いですが、どこを受けるにしても数的処理の出題数は多く、決して捨てることのできない科目です。
どのように学習を進めていけばよいのか。正攻法から、裏技まで述べていきます。
スポンサーリンク
1、定番の解法を覚える
中学受験を経験していない人にとって、数的処理の問題は「はじめて見る問題ばかり」です。
中学受験経験者にとっても、一部の問題は初体験でしょう。
初めて経験する類の問題がスラスラ解けないからといって不安になる必要はありません。
どんどん解答を見て、定番の解法を覚えていきましょう。
独力で、オリジナルの解法を生み出すことに情熱を燃やす必要はまったくありません。
そもそも、数的処理の問題がスラスラ解ける人というのは、定番の解法パターンが頭に入っている人なのです。
そういう人は、中学受験経験などで解法パターンの暗記訓練を過去に済ませているのです。今このときに、苦手だ嫌だ、と言っていてもはじまりません。どんどん定番の解法を覚えていきましょう。
2、解説を読んだ後、次にやるべきこと
あたりまえのことですが解説を読んで、「わかること」が第一歩です。
そして、わかった!と思って学習を終わりにしてはいけません。
その後がとてもとても大事です。
解説を読んでから少し時間を置いてみて、改めて1人で解けるかを確認することが大事です。
- 自力で答えまで辿りつけるのか、途中のどこかで詰まってしまうのかを知る。
- もし詰まってしまったのならば、改めて解説を読む。
- またしばらく経ってから、自力で解けるのかを確認する。
地道にこれを繰り返しましょう。
たくさんの問題を経験していくと、共通の解法を用いる問題であったり、似たような考え方をする問題であったりに出くわします。
数的処理の解法パターンなんて”たかが知れてるな”、”似たような問題ばかりだな”と思う日が必ずやってきますので、できれば毎日少しつづでも練習を繰り返していきましょう。
3、 解説読んでもわからないとき
どうしてもわからない、という問題もあるかもしれません。
以下の2つに大別できます。
- a.基礎力の欠如
- b.問題が難しい
a.基礎力の欠如
その問題がわからない理由が基礎に穴があることならばあたりまえですが、その穴を埋めるための努力を惜しんでいる暇はありません。
少なくとも中学生の数学までの内容はクリアーしていないと、スタート地点に着けないこともあり得ます。抜けている知識は、どんどん埋めていきましょう。
b.問題が難しい
中にはとても難しい問題もまぎれています。
どうしてもわからない問題は”いつか戻ってくるぞ”という印をつけておいて、とりあえず飛ばしましょう。
数か月後に読み直してみて解決できることもあります。また、最後の最後までよくわからなかった、という問題があっても実はOKです。
むしろ数的処理のあらゆる問題が一瞬で解ける、という受験生など皆無です。試験本番でも、出題数の6、7割が正解できればよいとも言われています(もちろん、他の科目の得手不得手次第です)。
4、書き出しの重要性
数的処理の学習方法として、「書き出し」の重要性を説きたいと思います。
主に、「場合の数」と「判断推理」で必要とされる能力です。
「能力」と書きました。「書き出し」とは幼稚な解法ではなくて、「能力」です。
場合の数
まず「場合の数」ですが、書き出し切ることが本質です。
順列や組合せの公式も、書き出しによる全容把握あってこそ、使いものになります。全容把握ができない人は、公式も上手に適用ができません。
また、書き出しきるしかない問題もたくさん存在します。
「場合の数」が苦手は人は、どんどん書き出しをする学習法を取ってください。
書き出しによって、部分的に公式が使える箇所が見えてくるような問題が主流です。
また、たくさん経験を積めば書き出さなくても頭の中だけで処理できる部分が増えていきます。
得意な人ほど書きだしていると言えます(その結果、全容把握をして、最後は計算で済みます)。
判断推理
次に「判断推理」です。「判断推理」の論理パズルのような問題群は、表などにまとめて論理的に詰めていく解法になります。
しかし、難しい問題になるとすぐには決定できず3、4通りの場合分けが必要になってきますね。
(例えば、Aくんの右隣にいる人の候補は、BかCかD、のような)
このようなときに、論理で詰め切ることにこだわるよりも、3通りの場合すべてを書きだしてしまった方が速いことも多々あります。
論理的に詰める訓練も大事ですが、いざという時に書き出しが有効であることは十分ご理解いただけると思います。
5、しょせんは5拓なので・・・あてはめ解法
数的処理は、選択肢から選ぶ形式です。
よって”選択肢を見ながら問題を解く”という方法があります。この方法はあらゆる問題で万能ではありませんが、一部の問題に有効であることは事実です。
当サイトで扱っている問題を実例として見ていきましょう。
速さ 問題5
Bは90mあるトンネルにAが入ってから4秒後に入り、Aが出てから3秒後に出てきた。
このとき、Aの速さとして正しいのはどれか。
- 5m/s
- 6m/s
- 7m/s
- 8m/s
- 9m/s
2011 地方上級
これはあてはめてしまった方が速い問題です。
(当サイトの解説では、2次方程式をたててから、選択肢をあてはめています)。
実際に5通りで調べると以下のようになります。
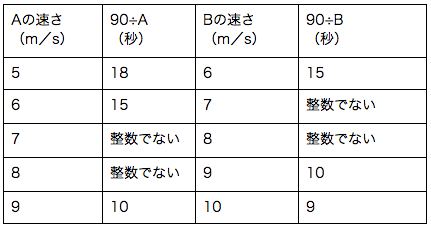
トンネルの通過時間はBの方が1秒短いので、 選択肢5が答えとわかります。
もう1問だけ実例をみておきましょう。
濃度 問題6
- A:ある重さの食塩水をビーカーから捨てる。
- B:Aで捨てた食塩水と同じ重さの純水をビーカーに加え、よくかき混ぜる。
- C:Aで捨てた食塩水の5倍の重さの食塩水をビーカーから捨てる。
- D:Cで捨てた食塩水と同じ重さの純水をビーカーに加え、よくかき混ぜる。
以上から判断して、Aで捨てた食塩水の重さとして正しいのはどれか。
- 15g
- 16g
- 20g
- 24g
- 25g
東京都 2009
はじめに溶けていた食塩の量は40g
最後に溶けていた食塩の量は18gです。
もし選択肢1が正しならば、
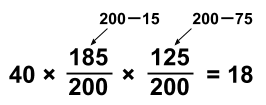
この等式が成立しないことは、実際に計算しなくてもわかりますね。
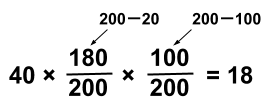
それに、選択肢のどれを選べば成立しそうかもピンとくるのではないでしょうか。
選択肢3のときに成立しますね。 正解は選択肢3です。
まとめ
上で取り上げた2題は、あてはめ解法がベストといってもいい2題でした。
他には
- あてはめでは解けないタイプ
- あてはめで答えを探すと、かなり面倒なタイプ
になります。
あらゆる問題で有効な方法ではありませんが、選択肢を考慮しながら問題を解き進めていくことはとても実践的なことです。
しかし、上の例を見てもお分かりかと思いますが、そもそもあてはめ解法をとるためにも、最低限の素養が必要です。
あてはめが速いのかどうかも、見極められないといけません。
学習初期はまっとうに問題を解く訓練が必須です。その後、実際の試験を見越した練習の時期に、あてはめ解法も考慮しながら問題を解いていきましょう。
これが最も有効な学習となります。
スポンサーリンク




