【確率】問題11

解答

解説

とても難しい問題です。
この問題を解くためは、問題１０と似ている、という直感が必要です。
勝負がつかずに、何回も操作が繰り返されていくとき、互いに以前の相手と同じような状況になります。それが繰り返されていく構造です。

では、この着眼点で解きましょう。
勝負がつかずにこの操作を繰り返しているとき、
以下の２つの状況があります。
１．相手が〇を引いた直後にカードをひく
２．相手が×を引いた直後にカードをひく
ＡもＢも、この２つの状況を繰り返していきます。

相手が〇を引いた直後にカードをひくとき、最終的に勝つ確率を \(P\)
相手が×を引いた直後にカードをひくとき、最終的に勝つ確率を \(Q\)
とします。
Ａの勝つ確率とＢの勝つ確率がそれぞれ \(P\) と \(Q\) でどのように表されるかを考察します。
Ａの勝つ確率を \(x\)
Ｂの勝つ確率を \(y\) とします。

１回目　Ａ

はじめのＡは、それ以前の人がひいたカードがなく（〇も×もない）
例外です
ちょっと置いておきましょう。

２回目　Ｂ

２回目はＢの番です。
１回目にＡが○を引いたＢが、その後勝つ確率は \(\displaystyle \frac{1}{2}×P\)
１回目にＡが×を引いたＢが、その後勝つ確率は \(\displaystyle \frac{1}{2}×Q\)
となります。

つまり、Ｂが勝つ確率 \(y\) は
\(y=\displaystyle \frac{1}{2}P+\displaystyle \frac{1}{2}Q\)・・・①
となります。

３回目　Ａ

３回目はＡの番です。
それ以前の2回がどうであったのかは、以下のア、イ、ウ、エの４通りです。

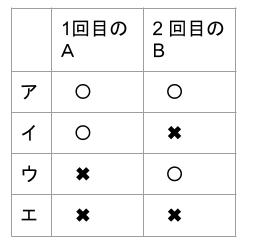
アの後Ａが勝つ確率

Ａがこの状況になる確率が\(\displaystyle \frac{1}{4}\)、その後勝つ確率は \(P\)
より、\(\displaystyle \frac{1}{4}×P\)

イの後Ａが勝つ確率

すでにＡの勝ちが確定です。このようにＡが勝つ確率は、\(\displaystyle \frac{1}{4}\) です。

ウの後Ａが勝つ確率

Ａがこの状況になる確率が\(\displaystyle \frac{1}{4}\)、その後勝つ確率は \(P\)
より\(\displaystyle \frac{1}{4}×P\)

エの後Ａが勝つ確率

Ａがこの状況になる確率が\(\displaystyle \frac{1}{4}\)、その後勝つ確率は \(Q\)
より、\(\displaystyle \frac{1}{4}×Q\)

Ａが勝つ確率 \(x\)

Ａが勝つ確率 \(x\) は

\(x=\displaystyle \frac{1}{4}×P+\displaystyle \frac{1}{4}+\displaystyle \frac{1}{4}×P+\displaystyle \frac{1}{4}×Q\)

\(=\displaystyle \frac{1}{4}+\displaystyle \frac{1}{2}P+\displaystyle \frac{1}{4}Q\)・・・②

この操作は、必ずＡかＢのどちらかが勝者になるので、
\(x+y=1\)
です。
より、①と②を用いて、①＋②＝１と表せます。

\(y=\displaystyle \frac{1}{2}P+\displaystyle \frac{1}{2}Q\)・・・①

\(x=\displaystyle \frac{1}{4}+\displaystyle \frac{1}{2}P+\displaystyle \frac{1}{4}Q\)・・・②

つまり、
\(\displaystyle \frac{1}{2}P+\displaystyle \frac{1}{2}Q+\displaystyle \frac{1}{4}+\displaystyle \frac{1}{2}P+\displaystyle \frac{1}{4}Q=1\)

整理すると、
\(4P+3Q=3\)・・・③
となります。
当然ですが、これだけでは解けません。
もう１つ立式できないといけません。

１回目　Ａ

ここで、はじめのＡから何か情報が得られないか考えてみましょう。
１回目のＡです。
Ａ以前には何のカードも引かれていないわけですが・・・

！！これは！！
２．相手が×を引いた直後　と同条件である！！
と気づきましょう。

自分が○を引こうが、×を引こうが、この時点では勝負が決まらない状態です。
スタート時点も、相手が×を引いた直後も、同条件なのです。

このことに着目して得られるＡの勝つ確率 \(x\) は
\(x=Q\)・・・④
です。
②＝④なので、
\(Q=\displaystyle \frac{1}{4}+\displaystyle \frac{1}{2}P+\displaystyle \frac{1}{4}Q\)

これを整理して、
\(3Q=1+2P\)・・・⑤
が得られます。

よって、③と⑤を連立して解きます。

\(4P+3Q=3\)・・・③
\(3Q=1+2P\)・・・⑤
これを解いて
\(P=\displaystyle \frac{1}{3}\)
\(Q=\displaystyle \frac{5}{9}\)
と求まります。

Ａの勝つ確率 \(x\) は \(Q\) と等しいので、\(\displaystyle \frac{5}{9}\)と求まりました。
先に引くＡがちょっとだけ有利ですね。