スポンサーリンク
問題
1からAまでの連続した整数をかけて数をつくります。このようにして作った数について、一の位から連続して並ぶ 0 の数を<A>で表します。
例えば、1×2×3×4×5=120 なので <5>の数値は1です。
<A>の数値にならない自然数のうち小さいほうから10番目を答えよ。
- 51
- 52
- 53
- 54
- 55
想定問題
解答と解説
解答
4
解説
1×2×3×4×5×・・・×A の中に素因数として5が含まれている数が<A>です。
<A>の数値がはじめて2になるのは、A=10
<A>の数値がはじめて3になるのは、A=15
<A>の数値がはじめて4になるのは、A=20
<A>の数値がはじめて5になるのは・・・
A=25 のとき、<A>の数値は6になります。
25(=5×5)は5を2つ含む数なので、<A>の値が2つ増えます。
つまり、このときに<A>の数値にならない数がでます。<A>の数値にならない最も小さい自然数は5 になります。
以上より、Aが25の倍数のときに<A>の数値にならない数がでるので、ここを調べます。
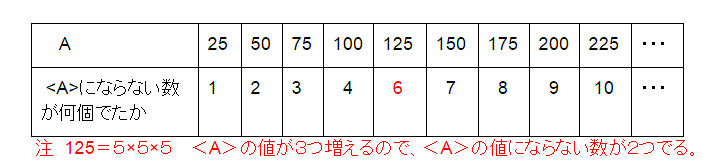
つまり、<224>=Nとすると、<225>=N+2 であり、求める10番目の数は N+1 です。
まずは<225>=N+2 を求めます。
1×2×3×4×5×・・・×225 の中に
5の倍数が45個、25の倍数が9個、125の倍数が1個あるため
<225>=N+2=45 +9+1=55
よって、求める10番目の数である N+1 は 54 です。
スポンサーリンク
