スポンサーリンク
問題
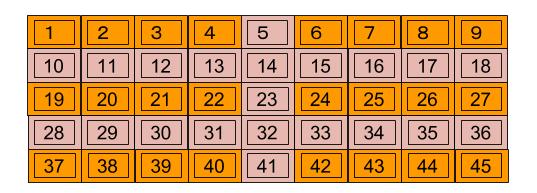
図のような5×9のブロックからなる長方形の板チョコをブロックの境目にそった直線で分け、A、B、Cの3人が順番に食べていきます。まず、Aが板チョコを二つの長方形に割り、片側をすべて食べました。次に、Bが残っている板チョコを二つの長方形に割り、片側をすべて食べました。同じように、C、A、Bの順番で、残っている板チョコを二つの長方形に割り、片側をすべて食べました。すると、残っている板チョコは1ブロックとなったので、それをCが食べました。このとき、3人は2回ずつ板チョコを食べたことになりますが、食べた板チョコの合計の大きさは3人とも同じであることがわかりました。
このとき、Cが食べた最後の1ブロックとして考えられないものを挙げているのはどれか。
ただし、選択肢の数値は図が示すブロックの位置です。
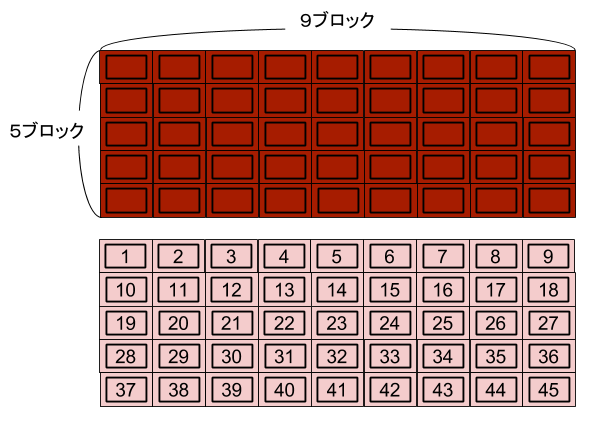
- 1
- 8
- 10
- 20
- 21
想定問題
解答
解説
45ブロックを3人が等しい量食べたので、3人はそれぞれ15ブロックずつ食べました。
よって、1回目のCは14ブロックを食べました。その板チョコの形は2×7のブロックしかありえません。
ここから先は様々なケースを調べていきます。
1回目のAの食べた板チョコは以下の3パターンしかありえません。
Aが5×1ブロックを食べる
1回目のCが2×7ブロック食べたことから、1回目のB、Cが決まります。
しかし、次にAが10ブロックを食べることができないため、このパターンではありません。
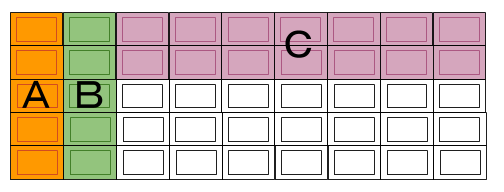
Aが5×2ブロックを食べる
1回目のCが2×7ブロック食べたので、1回目のBは、横の7ブロックを減らす食べかたはしません。
2回目のAが5個をとることから、1回目のBはCと同様に2×7ブロック食べました。
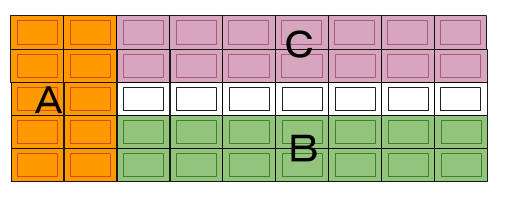
最後に残った1×7ブロックのうち、1×5をAが食べて、残った1×2ブロックを1ブロックずつBとCで分けます。
これが正解の食べ方です。
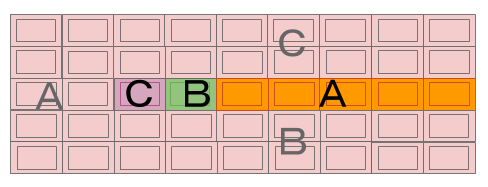
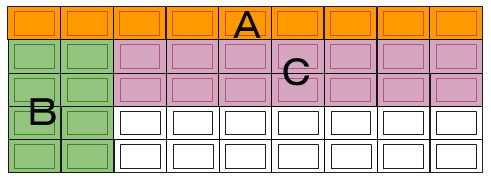
はじめにAが食べる場所は左右どちらでもよい。
その後のB、Cがどこを食べるか次第で、1×7ブロックは、1,3,5段目のいずれかに残ります。
その後のA、Bが左右どこを食べるか次第で、Cに残った最後の1ブロックの位置が変わります。
下図のオレンジ色の部分が、Cに最後に残り得る1ブロックの候補です。
問題の選択肢と見比べて、Cが食べたとは考えられないのは選択肢3の10です。
一応最後の候補がどうなるのかを検討しておきましょう。
Aが1×9ブロックを食べる
1回目のCが2×7ブロック食べたことから、1回目のBは横が7ブロック残るように食べます。
2回目のAが6個を2×3ブロックでしか取れないのですが、
すると、2回目のBが7ブロックを食べることができません。よって違います。
スポンサーリンク
