スポンサーリンク
問題
P地点とQ地点は1000m離れている。P地点からAが、Q地点からBが同時に出発した。AはQ地点に着くとただちに引き返し、BはP地点に着くとただちに引き返します。2人が1回目に出会った地点と、折り返して2回目に出会った地点とは300m離れていました。Aの方がBより速く、2人はそれぞれ一定の速さで進みました。また、2人が2回目に出会うまでに、AがBを追いこすこともありませんでした。
AとBの速さの比はいくらか。
- 5:3
- 9:7
- 11:9
- 21:19
- 23:17
想定問題
解答と解説
解答
5
解説
下の図のようになります。
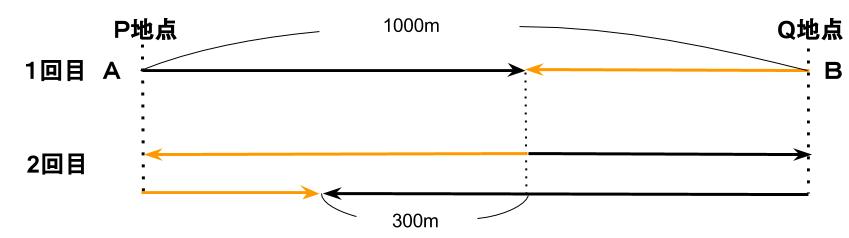
この問題のポイントは、
2人がスタートから1回目に出会うまでの時間をT分とすると、2人が1回目に出会ってから、2回目に出会うまでの時間は2T分になる
という点です。
2人の移動距離の和について見てみてください。スタートから1回目は1000m、1回目から2回目までは2000mと2倍になっています。
この点に着目して、方程式をたてます。下図のようにXm、Ymとおきます。
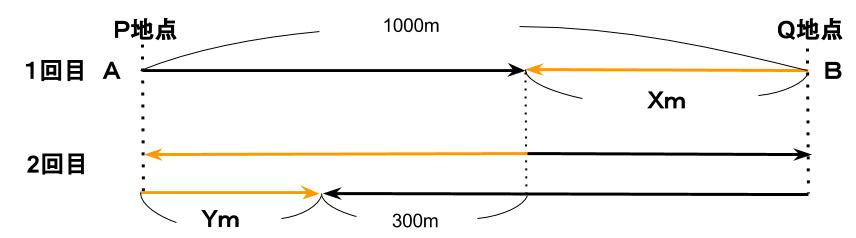
BがT分で進んだ距離はXm、次の2T分で進んだ距離は2倍の2Xmです。その2Xmは、図より(2Y+300)mと等しいので
2X=2Y+300
また、X+Y+300=1000・・・PQ間が1000mであるという立式
これを解いて、X=425、Y=275となります。
つまりはじめのT分で、Bは425m進み、Aは、1000-425=575m進みました。
2人の速さの比は、575:425=23:17です。
スポンサーリンク
