スポンサーリンク
問題
Aの容器には3%の食塩水が400g、Bの容器には10%の食塩水が600g入っている。今、A、Bそれぞれから同量ずつ食塩水を取り出し、Aから取り出したものをBへ、Bから取り出したものをAへ入れたところ、A、B2つの容器内の食塩水の濃度が等しくなった。このとき、A、B2つの容器から取り出した食塩水の量は、それぞれ何gずつか。
- 230g
- 240g
- 250g
- 260g
- 270g
2006 市役所
解答
解説
有名定番問題です。初見では気づきにくいポイントがありますが、もはや必須知識です。一度経験して、しっかり解法を覚えましょう。
下のようにまとめます。
はじめ Xgの交換後
A 3% 400g ⇒ Y% 400g
B 10% 600g ⇒ Y% 600g
この交換後のA,Bを混ぜると Y% 1000g になります。
この食塩水は、はじめのA、Bを混ぜたものと同一です。
これが初見では気づきにくいポイントです!
よって、濃さ3%の食塩水400gと濃さ10%の食塩水600gの混ぜ合わせでYが求められます。この問題ではYは聞かれていませんので、計算する必要はありませんが、ちなみにY=7.2 です。
(てんびん図などで確かめておきましょう。)
Yの値は主役ではありませんので、先に進みましょう。
主役は混ぜ合わせた食塩水の量の比です。
3%と10%を混ぜてY(7.2)%にしたかったら、混ぜる量の比が400:600=2:3でなければならないのです。
ここでAの容器に着目します(Bでも構いません)。
AからXgとりだして、BからXgいれた結果、Y(7.2)%になりました。
このとき、3%の食塩水と10%の食塩水を混ぜて、濃さをY(7.2)%にしているので、
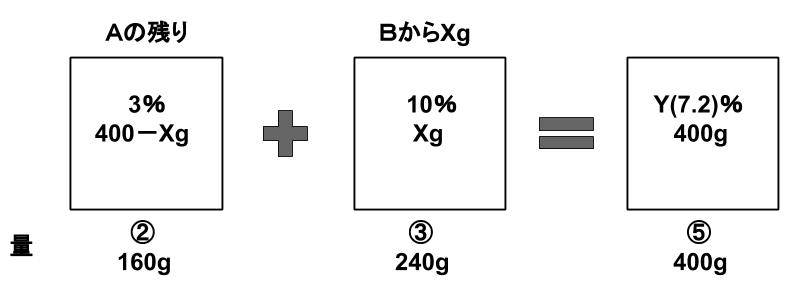
混ぜあわせた量の比は、2:3です。できあがった食塩水全体の量400gを2:3に比例配分すると160gと240gです。つまり3%の食塩水160gと10%の食塩水は240gを混ぜたことがわかります。交換した量、X=240gです。
※B着目でも同様の考察で解けますので、一度はやっておきましょう。
スポンサーリンク
