スポンサーリンク
問題
先日Pくんの通う学校で英語、数学、国語の試験が行われました。どの試験も25点満点で、点数はすべて整数でした。この試験を受けた200人の中で、P君は3教科とも平均点以上でした。P君の3教科合計の順位は、最も低くて何位と考えられますか。
- 195位
- 196位
- 197位
- 198位
- 199位
想定問題
解答
解説
前問と似ていますが、掴みどころがないですね。前問と違い、平均点が与えられていないからです。とにかくスタートを切りましょう。
平均点を仮に決めてみましょう。
仮に英語、数学、国語の平均点がすべて20点だったとします。Pも他の199人も全員が、3科目すべてで20点を取ったとして、スタートします。
Pの順位を下げるために、合計点が61点になる人を増やします。そのために、3科目すべて0点のQがいるとします。このとき、Pの順位は下のように、61位にできます。
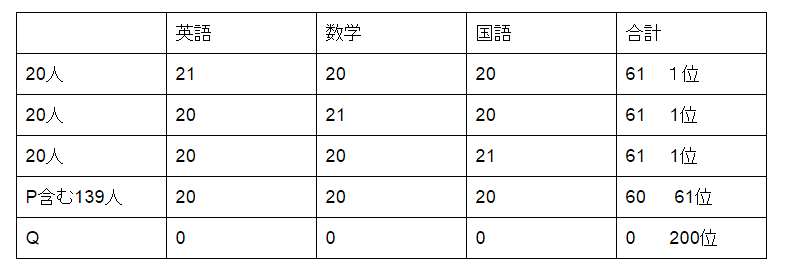
Qの持ち点が60点だったので、60人に1点ずつ分け与えられました。
持ち点が多ければ、より多くの人に1点ずつ分けられます。
より、英語、数学、国語の平均点がすべて24点だったとします。Pも他の199人も全員が、3科目すべてで24点を取ったとして、再スタートします。
Pの順位を下げるために、合計点が73点になる人を増やします。そのために、3科目すべて0点のQがいるとします。このとき、先の考察から72人をPより上位にできます。もう1人3科目すべて0点のRがいると、さらに72人をPより上位にできます。このときPは145位です。さらにもう1人Sの得点を下げることで、Q、R、Sの3人がPより下位、それ以外の196人はPより上位という状況をつくれます。Pは最低で197位です。
下にその1例を示します。
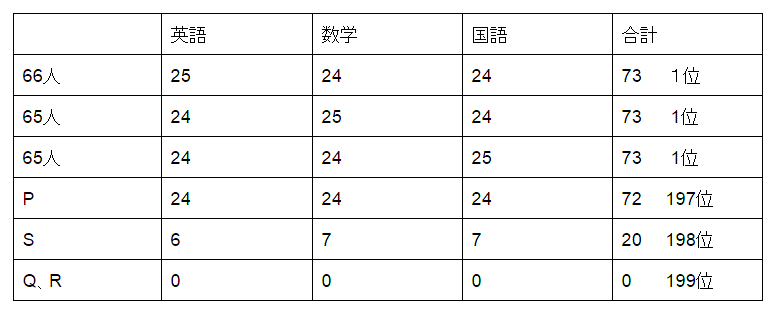
つまり、Pの下位になる3人が、Pより上位になる196人に点数を与えるような点数状況です。
よってPは197位になりえます。
スポンサーリンク
