スポンサーリンク
問題
12℃の水がでる給水栓と、一定の温度の湯がでる給湯栓が、それぞれ1個付いた浴槽がある。給湯栓を閉じて給水栓を全開にすると、空の状態から21分で浴槽が一杯になる。また、給水栓と給湯栓の両方を全開にすると、14分で一杯になり、そのときの浴槽の水温は32度になる。給水栓と給湯栓を同時に開けて42度の水温になるように最短時間で浴槽を一杯にする方法はどれか。
- 給水栓を全開にし、給湯栓の水量を全開時の1/2にする。
- 給水栓を全開にし、給湯栓の水量を全開時の2/3にする。
- 給湯栓を全開にし、給水栓の水量を全開時の1/2にする。
- 給湯栓を全開にし、給水栓の水量を全開時の2/3にする。
- 給湯栓を全開にし、給水栓の水量を全開時の3/4にする。
2012 特別区
解答と解説
解答
3
解説
仕事算と濃度の要素があり、どちらにカテゴライズするわけにもいかない総合問題なので、文章題全般にいれました。
浴槽一杯を時間(21と14)の最小公倍数を用いて42Xとすると、
それぞれの仕事量は下のようにまとめられます。
給水栓 2X/分
給水栓と給湯栓 3X/分
給湯栓 X/分
次に温度の考察をします。給湯栓からでる湯の温度をY℃とします。
給水栓と給湯栓の両方を全開にすると32℃になるので、上の1分あたりの仕事量より、
12℃の水とY℃の湯を、量の比2:1で混ぜると、32℃になるということです。
(これは、濃さが12%の食塩水と濃さがY%の食塩水を量の比2:1で混ぜると、濃さが32%になるのと同じ仕組みです。熱量・カロリーの仕組みです。)
下のてんびん図より、Y=72 です。
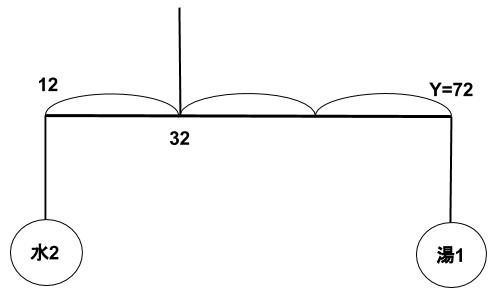
次に、12度の水と72度の湯を混ぜて、42度にすることを考えます。
下のてんびん図の通りで、水と湯の量の比が1:1で混ぜることになります。
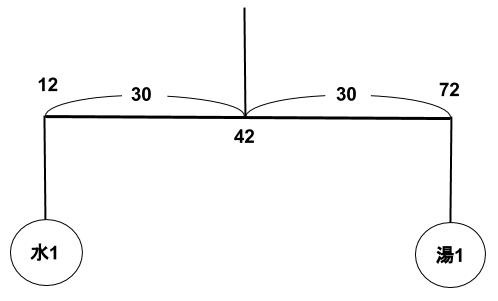
あとは選択肢5つを順に検討していきます。選択肢3のときに、水と湯の量の比が1:1になり、該当することが確かめられます。
スポンサーリンク
