スポンサーリンク
問題
A、B2人で行うとAだけで行うより12日間早く終了し、Bだけで行うより27日早く終了する仕事を、Aだけで行うとき、終了するまでにかかる日数として、正しいのはどれか。
- 18日
- 24日
- 30日
- 36日
- 42日
2008 地方上級
解答
解説
シンプルな問題文からは想像できないほど手ごわい問題です。多くの参考書の解説では、特に工夫のない未知数の置き方をした後、力技で方程式の処理をしているようです。
本サイトでは「この問題も仕事算なんだから、他の仕事算と同じような考え方で解きたい」
ということを主眼とした解説を載せます。
その結果、この問題の本質的な解法が見えてきます。
1日の仕事量を
- a/日・・・A
- b/日・・・B
- (a+b)/日・・・A+B
とする。全仕事量を ab(a+b)P ※計算のしやすいように設定
とすれば、それぞれがこの仕事にかかる日数は下のようにまとめられる。
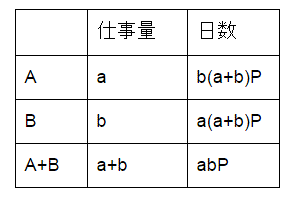
次に、日数の差について式にします。
2人で行うと、Aだけより12日はやい ⇒ b(a+b)P - abP =12・・・①
2人で行うと、Bだけより27日はやい ⇒ a(a+b)P - abP =27・・・②
①の左辺を簡単にして、b2P=12
②の左辺を簡単にして、a2P=27
の2式が得られます。
b2P=12 と a2P=27
これの比をとるとPが消えます。
a2P:b2P=27:12 よりaの2乗とbの2乗の比が27:12=9:4 です。
よって、a:b = 3:2 です。
これはAとBの仕事量の比なので、改めてまとめると下のようになります。
日数は、仕事量の逆比になりますね。
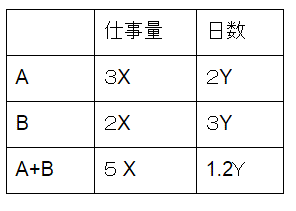
かかった日数の差より、3Y-2Y=15日 (下の線分図参照)なので、Y=15、これを用いて
全仕事量が90Xとわかる。

わかったことを改めて下にまとめます。
| 1日の仕事量 | 日数 | |
| A | 3X | 30 |
| B | 2X | 45 |
| A+B | 5X | 18 |
Aだけだと30日かかることがわかります。
最大公約数で割る ルートをとる
27 ⇒9 ⇒ 3
12 ⇒4 ⇒ 2
類題演習
A、B2人で行うとAだけで行うより50分早く終了し、Bだけで行うより1時間38分早く終了する仕事を、Aだけで行うとき、終了するまでにかかる時間はいくらか。
想定問題
解答
解説
98分と50分、公約数の2で割って、49と25。ルートをとれば、7と5。これが、AとBの1分あたりの仕事量の比です。
| 1日の仕事量 | 時間 | |
| A | 7X | 5Y |
| B | 5X | 7Y |
| A+B | 12X | 35/12 Y |
時間の差、2Y=48分なので、Y=24分
よって、Aだけで行うと5Y=120分 です。
| 1日の仕事量 | 時間 | |
| A | 7X | 120分 |
| B | 5X | 168分 |
| A+B | 12X | 70分 |
スポンサーリンク
