【ニュートン算】問題３

解答

解説

注意が必要です。
1日にのびる草の総量は一定ではありません。2倍の広さの土地には、２倍の量の草が生えます。
普通のニュートン算と同様に解くために、少し工夫をしましょう。
放牧する土地の広さが同じならば普通のニュートン算になるのですから、揃えてしまいましょう。

面積60アールの耕作放棄地に２頭の牛を放牧すると、180日で生えている草がすべてなくなった
とありますが、１頭ずつ30アールの土地に放牧しているのと同じ状況です。つまり、
面積30アールの耕作放棄地に１頭の牛を放牧すると、180日で生えている草がすべてなくなります。

これと、もう1つの放牧である、
面積30アールの耕作放棄地に２頭の牛を放牧すると、30日で生えている草がすべてなくなった。
この2つを線分図でまとめます。

また、最終的に求める状況は、
４頭の牛を面積100アールの耕作放棄地に放牧
ですが、
⇒面積30アールの耕作放棄地に1.2頭の牛を放牧　と言い換えられますね。

方針が決まりました。
いよいよ解きましょう。

１頭の牛が１日に食べる草の量をXとします。

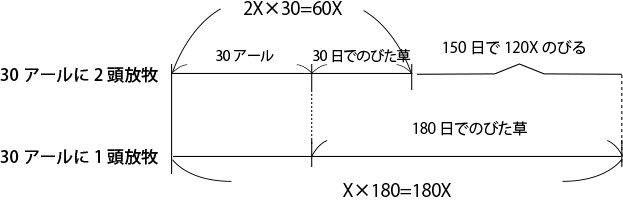
150日で増えた草＝120X　となり、
1日で増える草＝0.8Ｘ
はじめの30アールに生えている草＝36Ｘ　がわかります。

面積30アールの耕作放棄地に1.2頭の牛を放牧　の日数を求めるので、

36Ｘ÷（1.2Ｘ－0.8Ｘ）＝90日  と求まりました。

別解

上記でした工夫をしないと、以下のようになります。

１頭の牛が１日に食べる草の量をX
30アールの土地に1日にのびる草の総量を３Yとします。
問題文にある2通りの放牧は下のようになります。

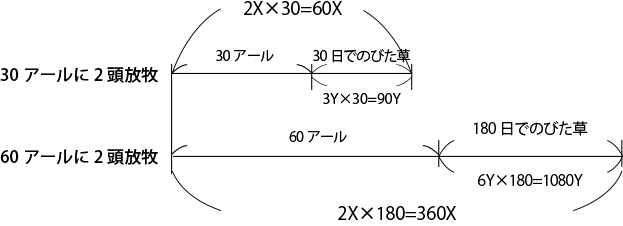
これはもう連立方程式をやるしかないですね。

• 上の線分図　⇒　60X＝30アール＋90Y・・・①
• 下の線分図　⇒　360X＝60アール＋1080Y・・・②

X、Y、アール、どれを消しても解けるのですが、②－①×２　でアールを消すと
240X＝900Y　となり、4X=15Y です。

これを用いて、改めて「30アールに２頭放牧」をXだけで表してみましょう。

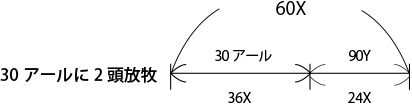
30アールに生えている草＝36X　であることがわかります。

全体像が分かったので、いよいよ「100アールに４頭放牧」です。

100アールに生えている草＝120X、
100アールの土地に1日にのびる草の総量が10Yなので

100アール÷（４X－10Y）＝120X÷（４X－８／３X）　※4X=15Y
＝90日