【確率】問題６

問題

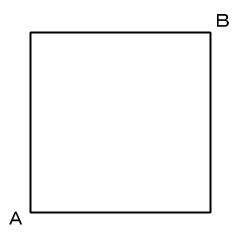
図のような正方形がある。頂点Aに駒をおき、サイコロを振り、出た目に応じ辺にそって隣の頂点に駒を移動させる。サイコロの目が１か２であれば上下に１つ移動させ、出た目が３から６であれば左右に１つ移動させる。サイコロを４回振って移動させたときに、駒が頂点Bにある確率はいくらか。

公務員数的処理KOMAROコマロ　場合の数　確率　　問題６　図１

裁判所事務　2012

解答と解説

４

図のように頂点C、Dとする。
奇数回移動させたとき、駒はＣかＤにいます。
偶数回移動させたとき、駒はAかBにいます。

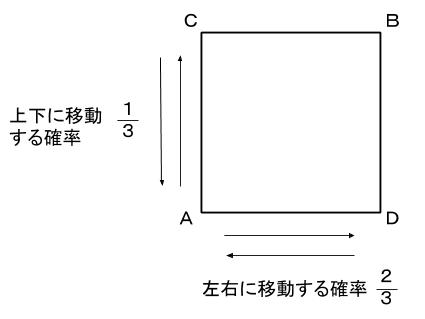
公務員数的処理KOMAROコマロ　場合の数　確率　　問題６　図２

まずは２回目にAにいる確率を求めます。
以下の２つ確率の和になります。
１．A→C→A
２．A→D→A

１．A→C→A
上下移動を２回連続なので、
1／３ × 1／３＝ 1／９

２．A→D→A
左右移動を２回連続なので、
２／３ × ２／３＝４／９

以上を合わせて、２回目にAにいる確率は５／９,
２回目にAにいない＝Bにいる確率は４／９です。

つまりある頂点から、２回でもとの頂点にもどる確率は５／９
対角線上の向かいの頂点に移る確率は４／９
とわかります。

続いて、4回目にBにいる確率を求めます。
以下の２つ確率の和になります。
１．２回目にA、４回目にB
２．２回目にB、４回目にB

１．２回目にA、４回目にB
先ほど求めた確率から、
５／９　×　４／９　＝20／81

２．２回目にB、４回目にB
同じく先ほど求めた確率から、
４／９　×　５／９　　＝20／81

以上より、20／81 + 20／81 = 40／81　となります。