【約数・倍数・素因数分解】問題２

問題

たて㎝、横㎝、高さが㎝の直方体があります。この直方体を同じ向きにすきまなく積んで、できるだけ小さな立方体を作るとき、必要な直方体の個数は何個ですか。　

想定問題

解答と解説

２

たて、横、高さのそれぞれの方向に直方体を何個ずつ積めばよいのかは、直方体のたて、横、高さの長さの比で決まります。

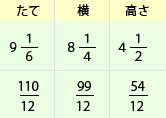公務員数的処理KOMAROコマロ　数　約数・倍数・素因数分解　問題2　図　※通分しました。

３辺の比が110：99：54の直方体です。
たて110、横99、高さ54の直方体を積んで、１辺の長さが110・99・54の最小公倍数となる立方体を作ります。

公務員数的処理KOMAROコマロ　数　数　約数・倍数・素因数分解　問題2　図

より、11×９×２×５×３が、求める立方体の１辺です。
よって下記のようになります。

上記より必要な直方体の個数は、27×30×55＝44550個です。