スポンサーリンク
問題
A~Fの6チームが、総当たり戦でサッカーの試合を行った。勝ちを2点、引き分けを1点、負けを0点として勝ち点を計算し、総勝ち点の多いチームから順位をつけ、総勝ち点で同点の場合は得失点差により順位を決めた。今、次のア~カのことがわかっているとき、3位になったのはどのチームか。ただし、同一チームとの対戦は1回のみとする。
ア Aは、BとEに負けた。
イ Bは、Dに負けなかった。
ウ Cは、A、E、Fと引き分け、得失点差によりAの下位となった。
エ Dに引き分けはなく、得失点差によりEの上位となった。
オ Fは、AとDに勝った。
カ 引き分けは4試合あった。
- A
- B
- D
- E
- F
特別区 2011
解答
解説
勝敗が分かっている箇所を星取表に埋めます。
また
イ:Bは、Dに負けなかった。
エ:Dに引き分けはなく、得失点差によりEの上位となった。
イとエの前半を合わせると、BはDに勝っていることがわかります。
ここまでが下図です。
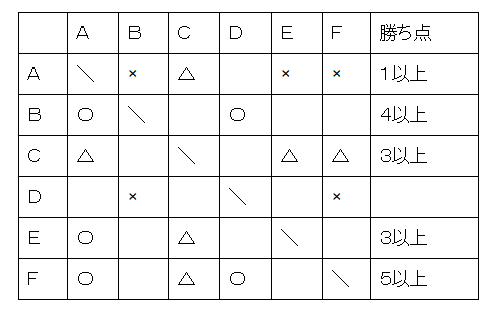
次に、
ウ:Cは、A、E、Fと引き分け、得失点差によりAの下位となった。
の後半です。
AとCは同じ勝ち点であったことがわかります。
その条件を満たすのは、
AがDに勝ち、CがB、Dに負けたときのみです。
ここまでが下図です。
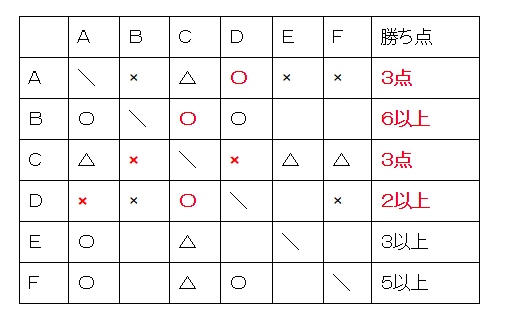
次に
エ:Dに引き分けはなく、得失点差によりEの上位となった。
DとEは同じ勝ち点であったことがわかります。
その条件を満たすのは、
DがEに勝ち、Eは残ったB,Fに対して1分け1敗のときです。
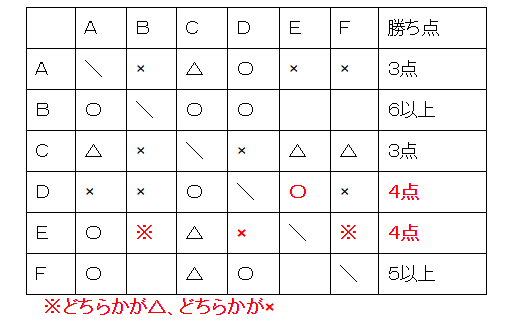
さて次ですが、EはBとFのどちらと引き分けたのだろうか・・・・?
それに
カ:引き分けは4試合あった。
この情報もまだ使っていません。
しかし、実はここから先は考える必要はありません。
本問は3位になったチームが分かればよく、星取表をすべて埋める必要はありません。
この時点ですでに順位は決定しています。
B、Fが1,2位です。どちらが1位なのかは直接対決の結果次第ですが、
考慮する必要はありません(実際に、決定できません)。
Aが5位、Cが6位も決定しています(得失点でCがAの下位とあります)。
D、Eが3、4位ですが、Dが得失点でEの上位とあるので、
Dが3位、Eが4位です。
よって、選択肢3、が正解となります。
スポンサーリンク
