スポンサーリンク
問題
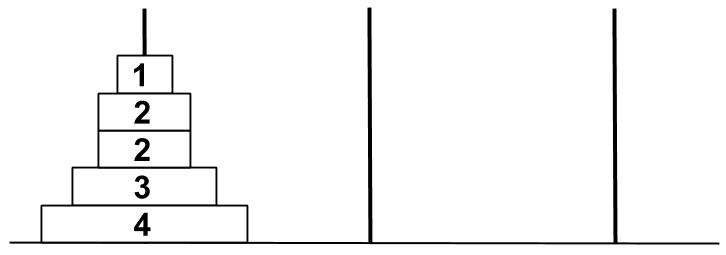
下の図のように3本の柱があり、そのうちの1本には中心に穴の開いた5枚の円盤が重ねられている。円盤に書かれた数字は円盤の半径の長さ(cm)を表している。この5まいの円盤を、次の条件を満たすように1枚ずつ別の柱へ移動させる。
・円盤は1回に1枚ずつ移動させる。
・小さい円盤の上にそれより大きい円盤を置いてはならない。同じ大きさの円盤は置いてよい。
このとき、5枚の円盤をすべて真ん中の柱に移すには、最低何回円盤を移動させなければならないか。
- 15回
- 19回
- 23回
- 27回
- 31回
想定問題
解答
解説
ハノイの塔とよばれる有名問題はご存じでしょうか。本問のような円盤を移していく設定の問題で、すべての円盤の大きさが異なるケースが本家ハノイの塔です。
ハノイの塔は、N枚の円盤の移動回数は、2のN乗-1 回という有名事実があります。
なぜこのようになるのかという原理を理解していない人を振るい落とすことも、選抜試験の目的ですから、本問のような変形が出題されることは多いに予想されます。
さて、この問題を解いていきましょう。ハノイの塔は、N枚を移すのがA通りとわかれば、N+1個を移すのが何通りなのかはすぐにわかる、という考え方で解く問題です。
高校数学の漸化式と似た考え方で、ドミノが次々に倒れていくような解法です。
当サイトではこの解法パターンの問題を【場合の数 ドミノ式】でたくさん紹介しています。
では、本問を解いていきましょう。
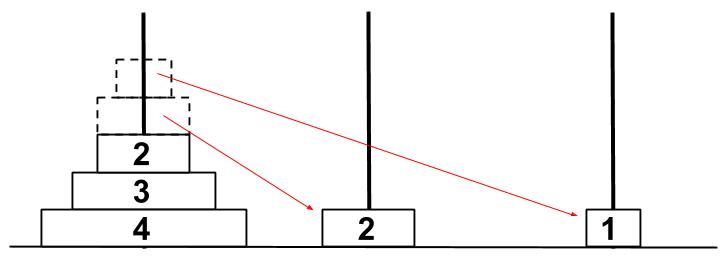
ここまで2回
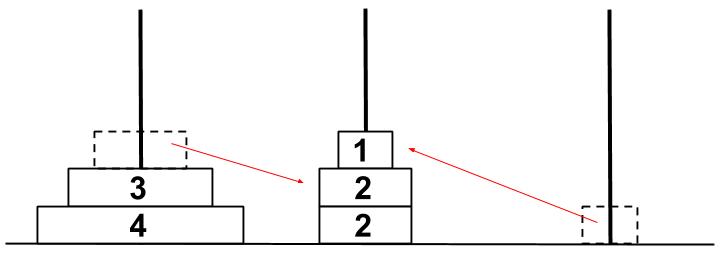
ここまで4回 (1,2,2)を別の棒に移すのに4回かかることが分かりました。・・・①
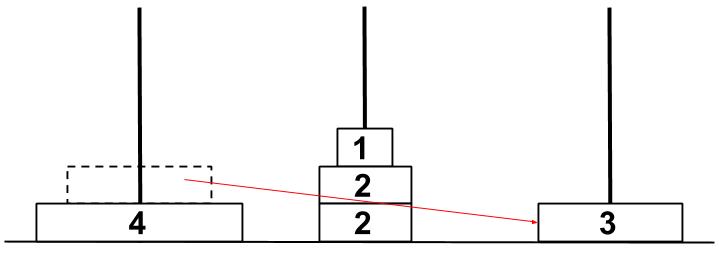
ここまで5回
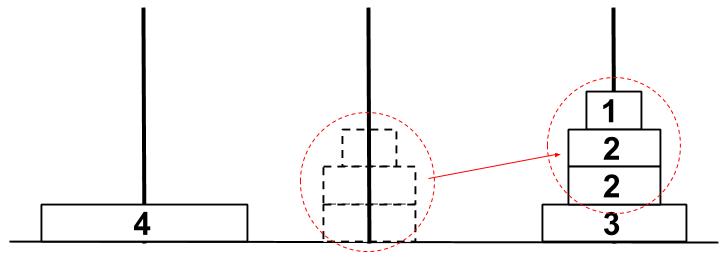
①より(1,2,2)を真ん中から右に移すのに4回かかります。
つまり、(1,2,2、3)を別の棒に移すのに9回かかることがわかりました。・・・②
ここまで9回です。
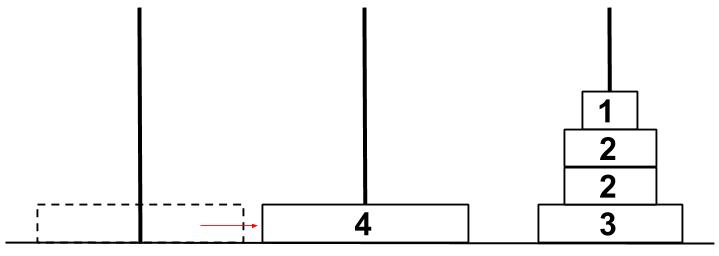
ここまで10回
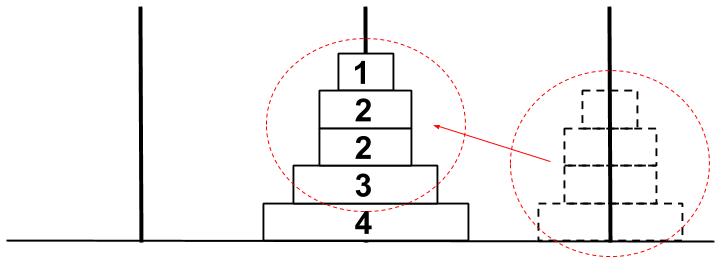
②より(1,2,2、3)を右から真ん中に移すのに9回かかります。
ここまで19回かかりました。
以上より19回です。
スポンサーリンク
