問題
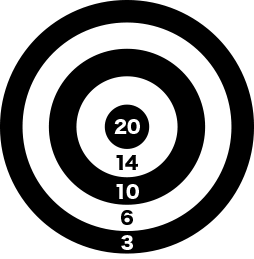
A~Dの4人が、次の図のような的にダーツを4回ずつ投げて、刺さった場所の数字が得点になるゲームを行った。この結果について、次のア~オのことが分かっているとき、確実にいえるのはどれか。ただし、ダーツが的を外れたことはなかった。
- ア:総得点は、Aが33点、Bが28点、Cが54点、Dが40点であった。
- イ:CとDが投げたダーツは、10点に2回ずつ刺さった。
- ウ:投げたダーツが同じ点数に2回刺さった人は2人いた。
- エ:投げたダーツが同じ点数に3回刺さった人は1人いた。
- オ:投げたダーツが同じ点数に4回刺さった人はいなかった。
- Aが投げたダーツは、20点に1回刺さった。
- Bが投げたダーツは、14点に1回刺さった。
- Cが投げたダーツは、14点に1回刺さった。
- Dが投げたダーツは、20点に1回刺さった。
- 投げたダーツが20点に刺さった人はいなかった。
2007 特別区
解答と解説
解答
3
解説
イとウより、投げたダーツが同じ点数に2回刺さった2人はCとDである。

あと2回で合計34点なので、20点と14点に1回ずつです。
※この時点で選択肢を見ると、3が答えであることがわかってしまいます。

あと2回で合計20点なので、14 点と6点に1回ずつです。
ここまでわかっていることは

エとオより、投げたダーツが同じ点数に3回刺さった人が1人、すべて異なる点数に刺さった人が1人です。
ダーツの5か所の点数の和が53点なので、20点を除く4か所にささると33点です。
この33点がすべて異なる点数に刺さったときの最低点なので、これがAと決まります。
よって、Bが同じ点数に3回刺さった人と決まります。
Bは28点なので、10点に1回、6点に3回刺さったと決まります。
以上より、すべて決まりました。
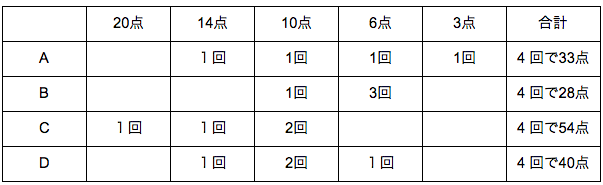
選択肢と見比べて、やはり3が答えと決まります。
スポンサーリンク
