問題
横に並んだいくつかのマスに○、△、×のいずれか1つを記入するとき、隣り合ったマスの少なくとも一方が○となるような記入の仕方を考えます。例えば2つのマスであれば、下図の5通りあります。
○○ ○△ ○× △○ ×○
条件をみたすように7マスを記入するとき、その記入の仕方は何通りあるか。
- 85通り
- 109通り
- 125通り
- 149通り
- 171通り
想定問題
解答と解説
解答
5
解説
左から右にマスをうめていくこととします。
1つ前のマスに何があるかで、次に記入できる記号が決まります。自由に記入はできません。
Nマス目に何があるかで、N+1マス目に記入できる記号が決まり、またその記号がN+2マス目に記入できる記号を決めます。まさしくドミノ式です。
よって、一番最後にある記号が何か、で分けて考えます。
一番右に〇を記入するためには、そのひとつ前はどの記号でも可能です。
つまり、Nマスの記入の仕方がA通りあれば、N+1マスの一番右に〇がある記入の仕方はA通り
一番右に△を記入するためには、そのひとつ前は〇のときだけ可能です。
つまり、Nマスの一番右に〇がある記入の仕方がB通りあれば、N+1マスの一番右に△がある記入の仕方はB通り
一番右に×を記入するためには、そのひとつ前は〇のときだけ可能です。
つまり、Nマスの一番右に〇がある記入の仕方がB通りあれば、N+1マスの一番右に×がある記入の仕方はB通り
下の表のようになります。
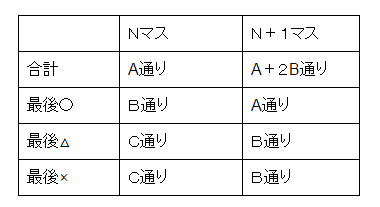
この規則に従って2マスから順にうめていきます。

よって、171通りです。
スポンサーリンク
