問題
正方形を21個使って、図1のような図形を作ります。次に、たとえば、図2のア、イのように、正方形の辺を使って長方形(正方形を含みます)を作ります。長方形は何個できるか。
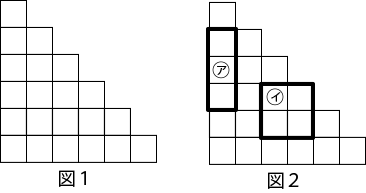
- 90個
- 108個
- 126個
- 135個
- 144個
想定問題
解答と解説
解答
3
解説
どのように数えれば場合分けや作業量を減らせるか。なかなか難しい問題です。
様々な数え上げ方がありますが、一例を示します。
長方形の4つの頂点のうち、右上と左下の点が決まれば、長方形は一つに定まります。
下図1で、黒点を右上の頂点とする長方形の数は6つです(単純に数えます)。
このように、各点に、その点を右上の頂点とする長方形の数、を書き込んでいきます。
0=ゼロは省略します。
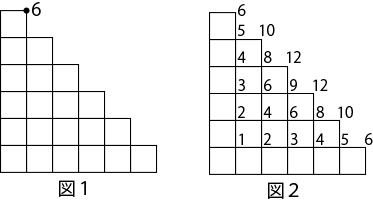
図2に書き込まれた数をすべて足せば答えです(縦一列の和が三角数、あるいは三角数の倍数になっていて、それ程面倒な計算ではないですね)。
答えは126通りです。
別解
衝撃的な別解を紹介します。衝撃としかいいようがありません。こんな解き方は普通は思い浮かびません。読後の爽快感を保障します。
問題の図を下図のように拡張します。9個の〇から4つを選びます。選んだ後、上から2つの〇からは下に線を引き、下の2つの〇からは左に線を引きます。これで4本の線に囲まれた長方形が1つできます。
つくられる長方形の個数は、異なる9個の点から4つを選ぶ組み合わせの総数と一致し、
9C4=126 と求まります。

スポンサーリンク
