基礎例題3
以下の方程式を満たす、自然数X、Yの組はそれぞれ何通りあるか求めよ。
5X+7Y=103
解答と解説
解答
3通り
解説
5X+7Y=103
問題1、問題2とはまた違ったタイプです。
このようなときに、
1の位に着目
というテクニックも知っておきましょう。
右辺の103の1の位は3です。
これは左辺の
5Xの1の位が0、
7Yの1の位が3
の和でつくることができそうです。
7Yの1の位が3になるのは、
7×9=63
がすぐに浮かびますね。
このとき、X=8、です。
よって、1組、解の組がわかりました。X、Y=(8、9)です。
あとは芋づる式に見つかりますね。
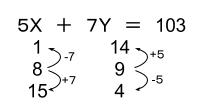
以上より、3通りです。
基礎例題4
以下の方程式を満たす、自然数X、Yの組はそれぞれ何通りあるか求めよ。
13X+9Y=200
解答と解説
解答
2通り
解説
13X+9Y=200
今まで学んだ方法、どれを使っても簡単には見つかりそうもないですね。
こんなときは最終兵器です。
左辺の係数のうち、小さい方に着目します。
今回はYの係数である9です。
この9で割ったときのあまりに着目します。
右辺の200は
200÷9=22あまり2 なので、
200=9の倍数+2
となります。
この2は、左辺の13X を9で割ったときのあまりが2であることを示しています。

より、あとは13の倍数を書き出して、9で割って2あまる数を探します。
13 26 39 52 65・・・
65が見つかります。
よって、X=5 このときのYを計算して、Y=15
あとは芋づる式です。
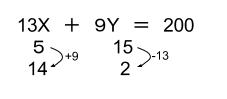
以上より、2通りです。
スポンサーリンク
