基礎例題1
3進法で1201は、10進法ではどのように表記されるか。
解答
解説
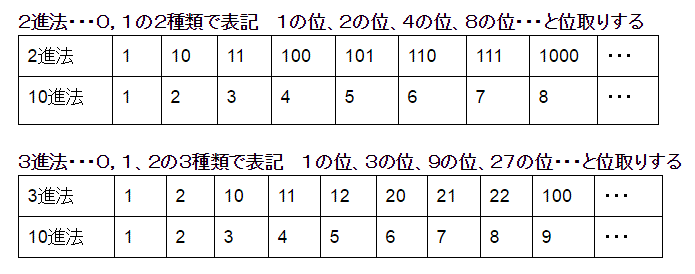
N進法とは、0,1,2・・・,N-1までのN種類の数字を用いて、
1の位、Nの位、Nの2乗の位、Nの3乗の位、・・・
と位取りをしていく数の表記方法です。
現在、我々が普通に使っているのは10進法です。
0~9までの10種類の数字を用いて、
1の位、10の位、100の位、・・・と位をあげる表記方です。
上のような説明を何回も読んでもピンとこないかもしれません。
具体的に10進法以外の表記方を見ていきましょう。
では問題を解いていきましょう。
根本原理がよく分からない人は、問題の解き方を先に覚えてしまえばOKです。
活用していくうちに、N進法の根本原理も理解できるようになります。
N進法を十進法へ
3進法の1201 ですが、各位が何を表しているかをまずおさえます。
それぞれ、3のN乗の位になっています。
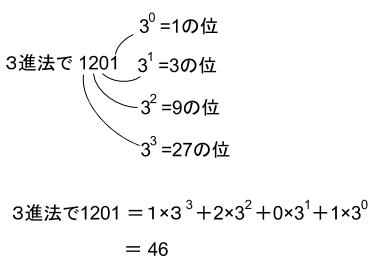
よって、27×1+9×2+0×3+1×1=46です。
基礎例題2
10進法で141は、4進法ではどのように表記されるか。
解答
解説
十進法をN進法へ はしご算
10進法の141を、4進法にします。
これは、はしご算で求めることがよく知られています。

なぜこれで求められるのか、については
下図のようになります。

十進法をN進法へ 定義通り計算
はしご算は機械的に求まって便利ですが、
やり方を忘れたときなどのために、原理原則にのっとって求める方法も
おさえておきましょう。
4進法の位取りは
・・・ 512 64 16 4 1
となっているので、
512以降の位は明らかに0
141÷64=2・・・13
より、64の位は2
16の位は明らかに0
13÷4=3・・・1
より、4の位は3、1の位は1
と順に求まります。
よって、
2031 と求まります。
基礎例題3
3進法で2202は、7進法ではどのように表記されるか。
解答
解説
このような問題では、直接変換することはできません。
必ず10進法を経由しましょう。
※原理的にできないわけではありません。
10進法以外の表記法の計算に習熟していれば可能ですが・・・無意味です。
よって、まずは
3進法の2202を10進法に直します。
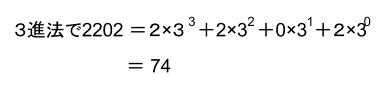
次にこの10進法の74を7進法表記にします。
はしご算でもよいですが、
定義通りの計算も楽です。
位どりは
49 7 1 なので
74=49×1+25
25=7×3+4
よって、134と求まります。
つまり、
74 = 49×1 + 7×3 +1×4
スポンサーリンク
