問題
下の表には、1~16の異なる整数が入り、また、縦、横、対角線上の4つの数の和はすべて同じになる。今、表のようにいくつかの数の配置がわかっているとき、AとBの数の積はいくらか。
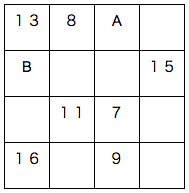
- 28
- 36
- 42
- 48
- 60
2006 国家Ⅰ種
解答と解説
解答
2
解説
まずは、4×4魔方陣の特徴を確認しておきましょう。
大原則1
縦、横、対角線上の4つの数の和は34です。
(1から16までの和)÷4=34 です。
大原則2
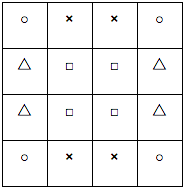
同じ記号をつけた4か所の数の和は必ず34である。
証明は省きます。インターネット上に4×4魔方陣の解説はいくらでもありますので、興味があればいろいろ調べてみて下さい。
ちょっと意識しておくとよいこと。
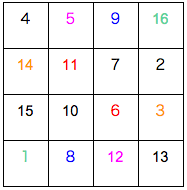
下の例は、中央の点に対して点対称な位置の2つの数の和が17になる魔方陣の例である。
すべての4×4魔方陣に成り立つ性質ではありませんが、このタイプの魔方陣の出題は非常に多く、下の例は、地方上級で2002年に出題されてものです。
すべての4×4魔方陣に成り立つ性質ではありませんが、このタイプの魔方陣の出題は非常に多く、下の例は、地方上級で2002年に出題されてものです。
さていよいよ問題を解きましょう。
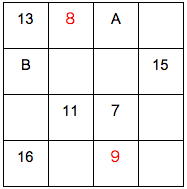
赤字を見てください。和が17です。
中央の点に対して点対称な位置の2つの数の和が17になる可能性大です。
これが成り立つとして魔方陣を埋めてみましょう。もしどこかで矛盾が見つかったとしても、たいした時間のロスではありません。
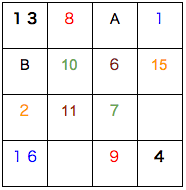
点対称の和17 でここまで埋まります。多分10秒くらいですね。残りは大原則1の一列の和が34で埋まります。
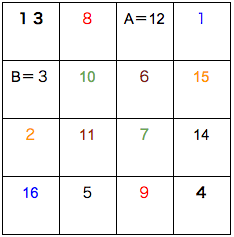
これで確定です。おかしなところもありません。
A×B=36です。
スポンサーリンク
