問題
1問が1点で、50点満点の入学試験がありました。この入学試験の受験者は100人で、結果は合格最低点31点、合格平均点40 点、受験者平均点34点でした。
この入学試験の合格者は、少なくとも何人以上はいると言えますか。
- 28人
- 30人
- 33人
- 38人
- 40人
想定問題
解答と解説
解答
5
解説
合格者をX人、不合格平均点をY点として、100人の合計点で立式すると
3400= 40X+ Y(100-X) Y≦30 (合格最低点が31点だから)
最小のXを求めることが目標である。
Xを少なくすると、40Xは小さくなるので、Y(100-X)は大きくしたい。
Y(100-X)を大きくするためには、Yも(100-X)も大きくしたい。
Xを少なくすると100-Xは大きくなるので、この点は問題は起きない。
よって、Yはできる限り大きいものを選べば、Xが最小となる。
合格最低点が31点なので、不合格平均点のY点は最大で30点である。
よって、3400= 40X+ 30(100-X)
これを解いて、X=40
別解
てんびん図で整理します。合格者をX人、不合格平均点をY点とします。
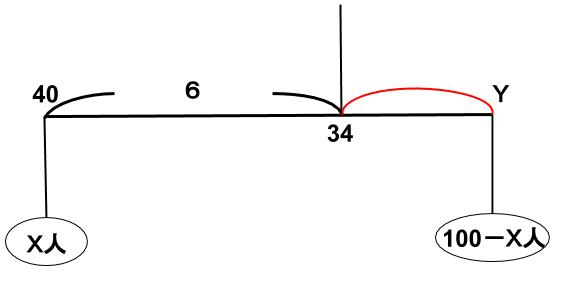
Xをできるだけ小さくしたい。 ⇒ 100-Xは大きくしたい。
よって、上のてんびん図の赤い長さをできるだけ短くする。
最大のY=30 なので、最小の赤い長さは4である。てんびんのつり合いを立式すれば、
6X=4(100-X)
X=40
スポンサーリンク
