問題
0,3,6、7をそれぞれ何個かずつ用いてつくられる数を小さい順に並べると
0 3 6 7 30 33 36 ・・・
となります。このとき、3776は、はじめから数えて何番目ですか。
- 125
- 126
- 127
- 128
- 129
想定問題
解答と解説
解答
3
解説
4種類の数字を使っているので、4進法です。
ただし、普通の4進法は0、1、2、3の4つを使いますが、本問は0,3,6,7の4つです。
変形4進法です。
変形4進法とはどのようなものか、下の表で対応を確認してみましょう。
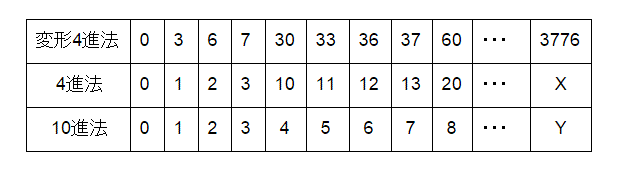
変形4進法と4進法の間で字の変換が必要です。
上の表のYに入る数を求めたいですね。
そのために、まずはXを求めます。
変形4進法で3776と表示される数は、4進法では、1332です。
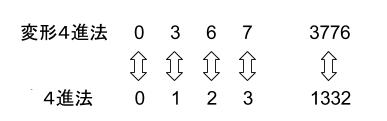
次にYを求めます。
4進法で1332と表される数を10進法になおします。
Y=64×1+16×3+4×3+1×2
=126
よって126番目!とすると間違いです。注意してください。
この数列は0からはじまっているので、127番目です。
別解
すべて4桁の数としてあつかいます。
0 ⇒ 0000
3 ⇒ 0003 のようにです。すると樹形図で解けます。
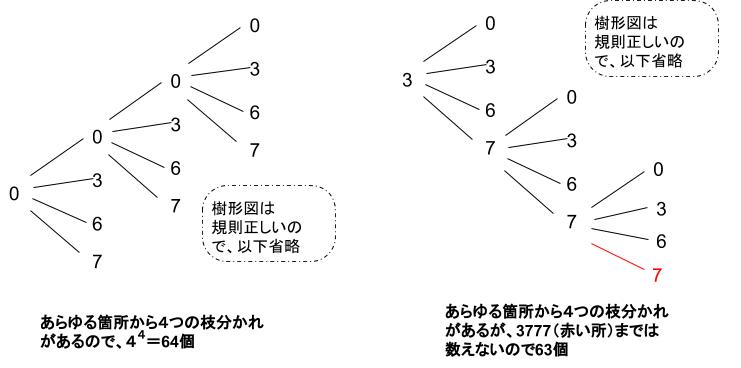
よって、64+63=127 と求まります。
スポンサーリンク
