姉妹サイト SPI非言語対策教室と同一内容です。
公式
まずは二つの公式を載せます。
順列
異なるn個のものからr個選び、並べる これを【 順列 】といいその総数は
![]()
組合せ
異なるn個のものからr個選ぶ これを【 組合せ 】といいその総数は
![]()
※r!=r×(r-1)×(r-2)×・・・×3×2×1
ポイント
この公式はもちろん大事ですが、公式丸暗記だけでは問題は解けません。どのようなときにどのように使えばよいのか、を理解・暗記することが最終目標です。
そのためには「全パターンを書き出す」ことからはじまります。
以下のような姿勢で問題に臨みましょう。
- 書き出しをすることで問題の全容を把握する
- 公式の正しい使い道が見える
- 結局は、全部書き出さなくとも、計算で答えがでる
しかし、次のようなパターンもあります。
- 書き出しをすることで問題の全容を把握する
- 公式が適用できないことがわかる。最後まで書き出しきるのみ
書き出し
基礎例題①
大小2つのさいころを投げます。出た目の和が8になるのは何通りですか。
解答と解説
解答と解説
5通り
『えーと、どっちの公式を使うんですか。』と考えずに、とにかく書き出しましょう。
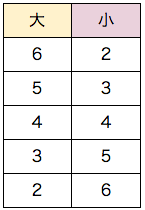
以上の5通りです。
重要
小さい順、大きい順、あいうえお順などのように、書き出しの際はルールを決めます。
小さい順、大きい順、あいうえお順などのように、書き出しの際はルールを決めます。
書き出しきってそれで終わりました。
このようにそもそも公式なんて通用しない問題もあります。まず、これを知っておいてください。
基礎例題②
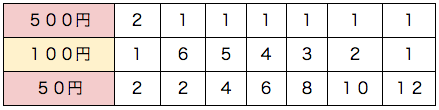
50円玉、 100円玉、 500円玉がたくさんある。この中から合計1200円になるような硬貨の取り出し方は何通りありますか。ただし、どの硬貨も少なくとも1枚は使うものとします。
解答と解説
解答と解説
7通り
これも書き出しで求めます。順列でも組合せでもありません。
決められた大きさ(1200円)を埋める問題は、まず大きいもの(500円)で埋めます。残りの隙間を小さいもので埋めるのは簡単です。
順列
いよいよ順列の公式が使えるケースがどのような場合なのかを見ていきましょう。
まずは書き出しをすることで公式の仕組みを理解しましょう。
基礎例題③
1,2,3,4,の4枚のカードから2枚をとりだして2桁の整数をつくると、何通りの整数ができますか。
解答と解説
解答と解説
12通り
まずは小さい順に書き出してみます。
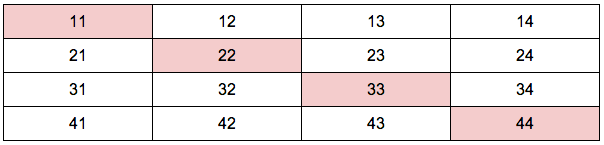
赤い背景部分はつくれません。同じ数字のカードが2枚ないからです。
よって、12通りになります。
基礎例題④
1,2,3,4,5の5枚のカードから3枚をとりだして3桁の整数をつくると、何通りの整数ができますか。
解答と解説
解答と解説
60通り
小さい順に書き出します。
123 124 125 132 134・・・ 何回も百の位の1を書くのは嫌になっちゃいます。以下のような書き方で省略しましょう。木の枝分かれのような図なので、樹形図といいます。
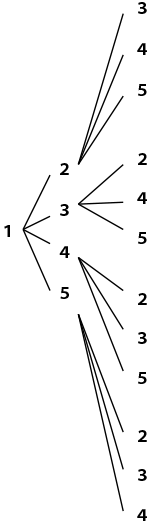
百の位が1のとき、12通りの整数がつくれました。
これはもしかして、百の位が 2 のときも、3 のときも・・・5通りすべてで12通りずつ作れますね!
これはもしかして、百の位が 2 のときも、3 のときも・・・5通りすべてで12通りずつ作れますね!
12×5=60通り 枝分かれする順にかけ算をかくと 5×4×3=60通り
この計算、5×4×3=60 が、冒頭に出て来た順列の公式そのものとなります。
異なるn個のものからr個選び、並べる
![]()
本問においては、異なる5個( n )のものから3個( r )選び、並べる。ということですね。
順列の公式は、樹形図を背景にしたものです。
順列の公式は条件付き問題になったとたん、使い方が分からなくなる人が多いです。公式丸暗記では今後対応しきれません。
上記の仕組みをきっちり理解してください!
全場合の数がどんな樹形図になるのか明確なイメージがわけば、どんなかけ算をすればよいのか自明になります。
※ここをきっちりと理解しておけば、確率の理解がスムーズになります。
順列の公式は条件付き問題になったとたん、使い方が分からなくなる人が多いです。公式丸暗記では今後対応しきれません。
上記の仕組みをきっちり理解してください!
全場合の数がどんな樹形図になるのか明確なイメージがわけば、どんなかけ算をすればよいのか自明になります。
※ここをきっちりと理解しておけば、確率の理解がスムーズになります。
基礎例題⑤
A、B、C、D、E、Fの6人でリレーをします。走る順序は全部で何通りありますか。
解答と解説
解答と解説
720通り
樹形図の全体像をイメージしましょう。(実際に書いてみるのもよいです。)規則正しく枝分かれしていきますね。
そのイメージがあれば、計算1発ですね。
6×5×4×3×2×1=720(通り)
答え 720通り
条件つき問題
条件がある場合、そこから決めていくことで効率よく調べきることができます。
基礎例題⑥
0,1,2,3の4枚のカードから3枚をとりだして、3けたの整数をつくると、何通りの整数ができますか。
解答と解説
解答と解説
18通り
異なる4枚から3枚を取り出して並べる、まさに順列の問題です。
しかし、【 0 】は、はじめ(百の位)におけない という条件が隠れています。
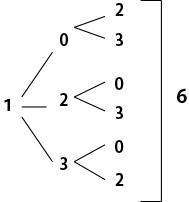
百の位が 2、3 のときも同様に6通りずつあるので、
6×3=18通りとなります
基礎例題⑦
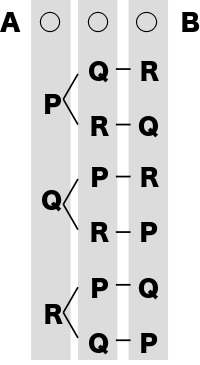
男子2人、女子3人の合わせて5人が一列に並んで写真撮影をする。
両端が男子になる並び方は何通りありますか。
両端が男子になる並び方は何通りありますか。
解答と解説
解答と解説
12通り
男子をA、B・女子をP、Q、Rとします。
男子の並び方は
A○○○B と B○○○A の2通りあります。
女子は○○○のところに並べます。
女子の並べ方は
3×2×1=6(通り)※順列ですね
よって、2×6=12(通り)
答えは12通りとなります。
この式【 2×6=12 】ですが、なぜかけ算なのか分からなくなった人はいませんか?
これも、樹形図の枝分かれだからです。A○○○B と B○○○A の2通りにそれぞれ6通りずつ枝分かれがあるからです。
基礎編②にで、最重要事項の組合せを学習しましょう。
スポンサーリンク
