【場合の数】問題７

解答

解説

選択肢５の２１０通り、で間違う人が多発する問題です。
以下、なぜ間違いなのかを解説します。

まず、どのように考えると２１０通りになるのかを再確認します。

７人から３人を選ぶ_７C_３＝３５（通り）

残った４人から２人を選ぶ、_４C_２＝６（通り）
残りの２人が自動的に２人グループになる。

３５×６＝２１０（通り）

申し分ない解き方ですが、一か所だけ落とし穴があります。
残った４人を２人ずつのグループに分ける分け方が６通りという箇所です。

実際に見てみましょう。
残った４人が、ABCDだとします。
この４人から２人を選ぶ組み合わせは、_４C_２＝６（通り）
で間違いないですが・・・

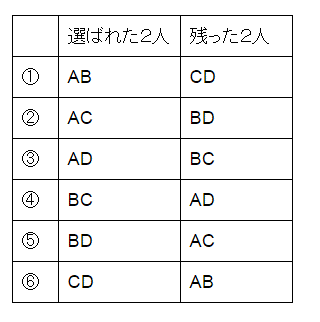
お気づきでしょうか。
①のグループ分けと⑥のグループ分けが同じです。
同様に②と③、④と⑤が同じグループ分けです。

つまり、４人を２人ずつのグループに分ける分け方は３通りです。
４人から掃除当番を２人選ぶなら６通りです。
グループに区別があるのか、ないのか、で分けかたの総数が異なります。
区別がないのならば、区別がある場合を重複の数で割ります。

よって、７人から３人を選ぶ_７C_３＝３５（通り）
残った４人を２人ずつのグループに分ける分け方は_４Ｃ_２÷２＝３通りずつ、
全部で３５×３＝１０５（通り）
となります。

解答

解説

まず、７人から１人を選ぶのが７通り。
ここまでは問題なしです。

つぎに、６人を２人ずつの３グループに分けるのが何通りなのか考えます。

残った６人から２人を選ぶのが_６C_２＝１５通り
さらに残った４人から２人を選ぶのが_４C_２＝６通り
全部で15×６＝９０（通り）
となりますが・・・もちろんまだ続きがあります。

いま計算した９０通りは、
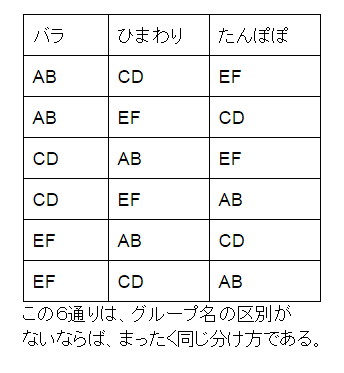
バラ組の２人、
ひまわり組の２人
たんぽぽ組の２人
のように、グループに区別がある場合です。
本来は、まったくグループに区別がないので、重複して数えている回数で割ります。
重複回数は３×２×１＝６（回）なので、
９０÷６＝１５
６人を２人ずつの３グループに分けるのは１５通りです。

よって、７×１５＝１０５通りです。