問題1
図のような経路で、点Aを出発して点Pを通り点Bへ行く最短経路は何通りあるか。
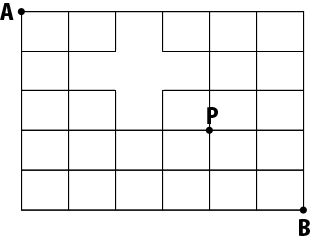
- 40通り
- 48通り
- 54通り
- 60通り
- 72通り
2010 国家Ⅱ種
解答と解説
解答
3
解説
あまりにも有名な問題です。ドミノ式解法の最たるものとして筆頭にあげないわけにはいきません。各交差点に、出発点からその交差点までいく最短経路の数をどんどん書き入れていく解法です。最短経路なので、進める方向は右か下です。左や上に進んではいけません。
下図のようになります。
例えば、点Eにいく経路の数は、点Cからと点Dから行くしかないため、点Cまでの経路の数3通りと点Dまでの経路の数4通りの和、7通りとなります。
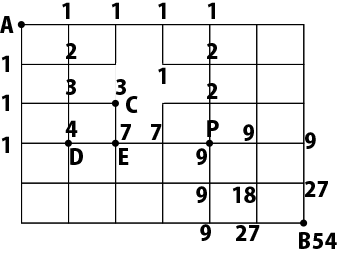
求める答えは上図より54通り
この解法は、「直前の結果を利用して次がわかる。その結果を利用して、その次がわかる」というドミノ倒しのような仕組みになっています。
このドミノ倒しのような仕組みを利用して解く問題をこれから順に見ていくことで、ドミノ倒し解法を極めましょう。
スポンサーリンク
