【確率】問題10

解答

解説

Ｃが勝つケースは、無限にあることがわかりますか？
いつまでもいつまでも勝負がつかないことが起こりうるからです。
大相撲の巴戦（３人による優勝決定戦）に似ている状況です。
※巴戦の確率も有名問題なので、知っておいて損はありません。

Ｃが勝つパターンとその確率は、以下のようになります。

よって、Ｃの勝つ確率をＳとすると、Ｓはこれらの確率の和なので以下の式のようになります。
これは等比数列の和と呼ばれるものになっています。

等比数列の和は、無限個であっても計算することができます。
以下のような考え方をします。

これを解いて、Ｓ＝４／１９と求まります。
以下の別解も必ず学習しておきましょう。

別解

Ａの勝つ確率はいくらになるでしょうか。
Ｂの勝つ確率はいくらになるでしょうか。

先ほどＣの勝つ確率を求めたときと同様の考え方で求めることができます。

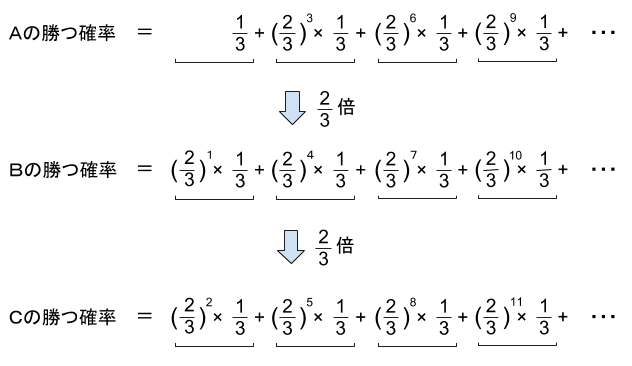
ところで、Ａ、Ｂ、Ｃの勝つ確率を求める式は、どれも似たような構造になっています。
等比数列の和を求めるときと同じ考え方で、
Ａの勝つ確率の２／３倍が　Ｂの勝つ確率、
Ｂの勝つ確率の２／３倍が　Ｃの勝つ確率、
になっていることがわかります。

つまり、
Ａの勝つ確率をＰとすると、
Ｂの勝つ確率は２／３×Ｐ
Ｃの勝つ確率は２／３×２／３×Ｐ＝４／９×Ｐ
となります。

3人のうち、いずれかが勝つので、この確率の和は１になります。
よって、
Ｐ　＋　２／３×Ｐ　＋　４／９×Ｐ　＝１
より、Ｐ＝９／１９・・・Ａの勝つ確率
これより、
Ｂの勝つ確率は６／１９
Ｃの勝つ確率は４／１９
と求まります。

式で厳密に考察をしてきましたが、端的にこの問題をとらえると
はじめにＡは２／３の確率ではずれを引きます。
このときＢは、はじめのＡと同じ条件に立てます。
つまり、Ｂは２／３の確率でＡと同じになるのです。
Ｃも同様で、２／３×２／３の確率でＡと同じになるのです。
これが、先の解き方で出てきた式の意味するところになります。
Ｐ　＋　２／３×Ｐ　＋　４／９×Ｐ　＝１
※ＰはＡの勝つ確率