問題
ある集団に対し、食事の好みについてアンケートしたところ、ア~エのことがわかった。このとき、確実にいえるのはどれか。
ア 焼き肉が好きな人は、ラーメンが好きである。
イ ラーメンが好きな人は、ケーキが好きでない。
ウ キムチが好きでない人は、ビールが好きでない。
エ ケーキが好きでない人は、キムチが好きである。
- 焼き肉が好きな人は、ビールが好きである。
- ラーメンが好きな人は、キムチが好きではない。
- キムチが好きでない人は、ラーメンが好きである。
- ケーキが好きな人は、焼き肉が好きでない。
- ビールが好きな人は、ケーキが好きである。
解答
解説
このタイプの問題は論理式による解法が最も代表的です。
以下、論理式について詳しく説明をしていきます。
1.命題と論理式
まず、ア焼き肉が好きな人は、ラーメンが好きである。
の意味するところから確認します。
※このような文を命題といいます。命題とは何か、まったく知らなくて結構です!
焼き肉が好きか嫌いか、ラーメンが好きか嫌いか、について分類すると以下の4タイプあることになります。
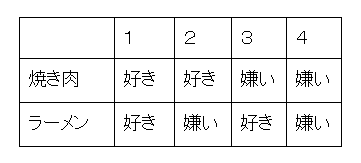
今回アンケートを取った集団においては、
ア「焼き肉が好きな人は、ラーメンが好き」なので、
この集団の中には、「焼き肉が好きで、ラーメンが嫌い」な2の人はいません。1の人がいます。
3や4の人がいるのかどうかについては不明なのです。
いるかもしれないし、いないかもしれない。どちらとも確実にはいえません。
この、焼き肉が好きな人は例外なく全員ラーメンが好きである、ということを
焼き肉 → ラーメン
のように表記してしまいましょう。
この表記方法が論理式です。省略表記しただけです。
続いて
イ「ラーメンが好きな人は、ケーキが好きでない。」
を論理式で表現します。
ラーメン → ケーキ
となります。
ケーキがケーキが好きの否定の表記方法です。
この論理式でア~エを表記すると
ア 焼き肉 → ラーメン
イ ラーメン → ケーキ
ウ キムチ → ビール
エ ケーキ → キムチ
簡単ですね!
2.三段論法
論理式の性質として p→q と q→r が成り立つとき、qを中継して、2つの式を1つにまとめることができます。
つまり、p→q→r が成り立ちます。
このとき、p→r ももちろん成り立ちます。
ソクラテスは人間である。
すべての人間はいつか死ぬ。
ゆえに、ソクラテスはいつか死ぬ。
が有名ですね。
三段論法はもちろん、4つ5つといくらでも繋げることが可能です。
この性質を利用して、ア~エを繋げてみましょう。
焼き肉 → ラーメン → ケーキ → キムチ
アとイとエは繋がりましたが、
ウ:キムチ → ビール
が繋がりません。
3.対偶
p → q が成り立つとき、q → p が成り立つ、ことが知られています。
q → p を p → q の対偶と呼びます。
対偶を考えることはとても多く重要です。しっかり覚えましょう。
ウ:キムチ → ビール の対偶は ビール → キムチ となるので、他の論理式と繋げられます。
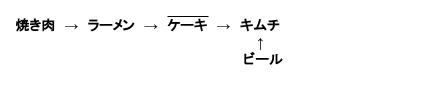
これを見ながら、1から5について検討していきます。
1:焼き肉が好きな人は、ビールが好きである
焼肉とビールの相性は抜群で、なんとなく正しい気がしますけども、論理の問題として解きます。
焼肉 → ビール という結びつきはつくれませんので、確実とはいえません。
2:ラーメンが好きな人は、キムチが好きではない
ラーメン → キムチ なので、これは明らかな間違いです。
3:キムチが好きでない人は、ラーメンが好きである
ラーメン → ケーキ → キムチ
は成り立っています。これの対偶をとると
キムチ → ケーキ
ケーキ → ラーメン
よって、 キムチ → ラーメン
キムチが好きでない人は、ラーメンが好きでないので、明らかな間違いです。
4:ケーキが好きな人は、焼き肉が好きでない
焼き肉 → ラーメン → ケーキ
は成り立っています。これの対偶をとると
ケーキ → ラーメン
ラーメン → 焼き肉
よって、ケーキ → 焼き肉
これは確実にいえます。正解は4です。
5:ビールが好きな人は、ケーキが好きである
ビール → ケーキ という繋がりはつくれません。
よって、確実とはいえません。
スポンサーリンク
