問題
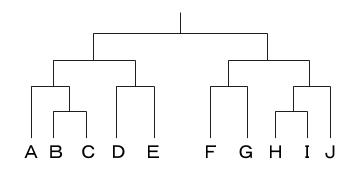
図のようにA~Jの10チームによるサッカーのトーナメント戦が行われ、この結果について次のアとイがわかっているとき、決勝戦の勝敗としてありうるのはどれか。
ア 3勝したのは2チームであった。
イ 初戦で敗退したのは5チームであった。
- AがJに勝った。
- CがIに勝った。
- DがGに勝った。
- FがBに勝った。
- HがEに勝った。
国税専門官 2001
解答と解説
解答
4
解説
イ:初戦で敗退したのは5チームであった。
よりAとJのどちらか片方は初戦敗退、どちらか片方は初戦を勝利しています。
AかJかどちらが勝ったのかはわからないので、下図のようにまとめます。
チームは上か下かのどちらか一列になります。
※トーナメントを2通りかくよりも楽ですね。
また点線の〇で囲まれた2チームは、互いに入れ替わりがありえます。
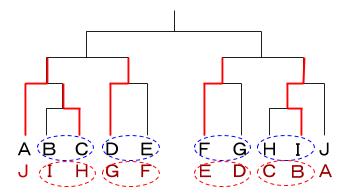
次に
ア:3勝したのは2チームであった。
を考察します。どのような試合結果だと
アの条件を満たすことになるのか。
準決勝に勝ち上がっている4チームの勝利数は、左から
1勝 1勝 1勝 2勝
となっています。
この後、準決勝で2勝、決勝で1勝の計3勝を4チームに振り分けることになります。
優勝する1チームに+2勝
準優勝の1チームに+1勝です。
3勝が2チームになるためには、
左から
3勝(優勝) 1勝 1勝 3勝(準優勝)
か
1勝 3勝(優勝) 1勝 3勝(準優勝)
になるかしかありえません。
よって、下の図のようになります。
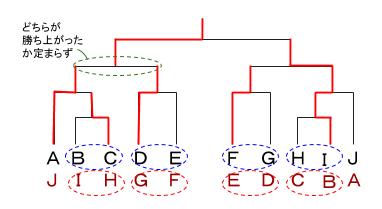
より、決勝戦は
ADE のいずれかが、HIのどちらかに勝った(6通り考えられます)。
あるいは、
JGF のいずれかが、BCのどちらかに勝った6通り考えられます)。
の全12通りがありえます。
選択肢を見ると
選択肢4のFがBに勝った
のみあり得ます。
スポンサーリンク
