問題
5人の小学生がそれぞれ花柄のリボンと水玉のリボンのどちらか片方だけを何本かずつ持っていて、その本数や種類について話しています。Aを除く4人は、自分以外の人のことを話しています。
- A: 5人の持っている合計本数は、花柄も水玉も20本です。
- B: Aはリボンを6本持っています。
- C: 一番リボンを多く持っている人は、水玉を12本持っています。
- D: 水玉を持っている人はEの他にもう1人います。
- E: Cの2倍、4倍の本数のリボンを持っている人がいます。
このときDはリボンを何本持っていますか。
- 7本
- 8本
- 9本
- 10本
- 11本
想定問題
解答と解説
解答
5
解説
Bの発言、Aはリボンを6本持っています。
Dの発言、水玉を持っている人はEの他にもう1人います。
より、
Aが水玉だとEは水玉を14本持っていることになりますが、これは
Cの発言、一番リボンを多く持っている人は、水玉を12本持っています。と
矛盾します。
よって、Aは花柄を6本持っています。
またC、Dの発言より水玉は8本持っている人と12本持っている人の2人(Eと誰か1人)です。
もし、Cが水玉ならば、Eの発言から、Cの4倍、最低8×4=32本持っている人がいることになり、これは矛盾しています。
よって、Cは花柄です。
Dの発言から、D自身は水玉を持っていません。
残ったBが水玉です。もちろんDは花柄です。
ここまでを表にまとめます。
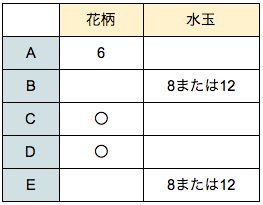
この表を見ながら考えます。
Eの発言、Cの2倍、4倍の本数のリボンを持っている人がいるので、この条件に当てはまるCの本数を探します。
- Cが1本だと、2本、4本の人がいる。 これは無理
- Cが2本だと、4本、8本の人がいる。 このとき4本はDとなるが、花柄の合計が20本にならず不適
- Cが3本だと、6本、12本の人がいる。 これは可能
- Cが4本以上だと、16本以上持つ人がいることになり、12本が最多であることに矛盾
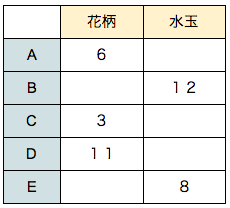
よって、Cが3本で確定です。Dは花柄の合計20本からAとCの和9本を引いて、11本です。
ちなみに、EはCの2倍、4倍の本数を持っていないので(自分のことを発言していないため)
Eは8本と確定します。下の表のようになります。
スポンサーリンク
