問題
23個のおはじきがありました。
A、B、C、D、Eの5人でじゃんけんをして、勝った人から順番に好きなだけおはじきを取っていったところ、全員の取った個数が異なりました。また、5人は以下のように話しています。
- A:私は、残りの半分を取りました。
- B:私は、残りを全部取りました。
- C:私は、2個取りました。
- D:私は、5個取りました。
- E:私は、残りの1/3を取りました。
3番目に取った人の個数と、4番目に取った人の個数はそれぞれ何個ですか。
- 4個 2個
- 4個 3個
- 3個 2個
- 3個 4個
- 3個 5個
想定問題
解答と解説
解答
3
解説
はじめに取ったのはA、B、Eではないことは明らかです。また、最後に取ったのがBです。
ここから先は、膨大な場合分けをしないためには、数の感覚が必要です。
全員の取った個数が異なるという条件から、次の2つが確定します。
- Eの直後にAがとることはない。直後だと、EとAは同じ個数になるため。
- Aの直後にBがとることはない。直後だと、AとBは同じ個数になるため。
以上のことから考えうる5人の取った順番は以下の4通りがあります。
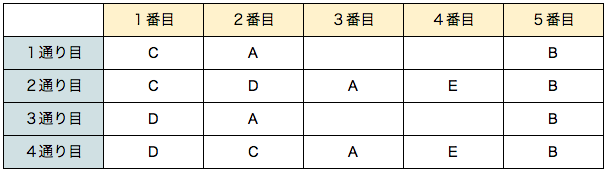
それぞれの場合について、おはじきがどのように分けられていくかを、順に調べていきます。
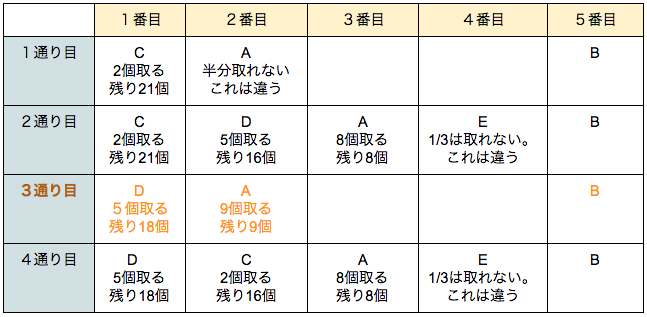
3通り目のみが可能です。
よって、下記の2通りが候補であるとわかります。
- D A E C B
- D A C E B
D A C E Bの順で取ると、Eが残りの1/3を取れません。
D A E C Bの順で取ると、順に5個、9個、3個、2個、4個と取っていったことがわかります。
スポンサーリンク
