問題
A、B、C、Dの4人が文化祭の準備で絵をかきます。筆は2本しかないので、常に2人が作業するようにして、交代しながら2人が休みます。休んでいるときは必ず、1人はゲーム、1人は本を読みます。以下のような条件で、絵の完成まで2時間かかりました。
・Aはゲームをせず、Cの5倍の時間本を読みました。
・Bは本を読んだ時間の3倍ゲームをし、本を読んだ時間とゲームをした時間の差は40分でした
・Cがゲームをした時間は、Bが本を読んだ時間と同じでした。
・Dが本を読んだ時間とゲームをした時間は同じでした。
・ゲームをするのも本を読むのもそれぞれ1人1度までとします。
Aがはじめに休んだとすると、AとDの2人が同時に絵をかいていた時間が何分間か。
- 0分間
- 10分間
- 20分間
- 30分間
- 40分間
想定問題
解答
解説
Bの情報から、Bはゲームを60分、本を20分とわかります。よって、残り40分が作画の時間です。
またCのゲームの時間は、Bの本の時間と同じなので20分とわかります。
下の表のように埋まります。
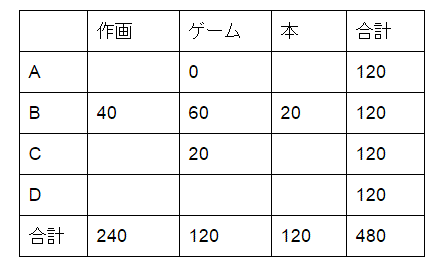
この表のゲームの列より、Dのゲームの時間は40分です。またDのゲームと本は同じ時間なので、40分ずつです。また、Aの本の時間とCの本の時間の比が5:1です。これを入れると
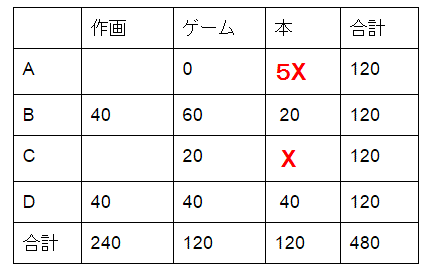
本の列をみると、Aの本は50分、Cの本は10分とわかります。
よって、残りの作画の時間も埋まります。
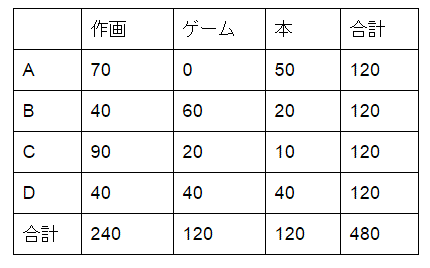
ここからはこの表を見ながら、4人が順に何をしたのかをあてはめで探します。
どこからどのように攻めればうまくいくのか、試行錯誤をするしかありません。
・ゲームと本は1人1度までである。
・同時間に1人が2つのことを同時にやることはない。
この2つと矛盾が起きるか起きないかを見ていきましょう。
ゲームの最後が誰なのかに着目します
Aがはじめに休んでいる(本を読んでいる)ため、Bがゲームの最後だとすると、Bが20分本を読む時間がとれないことがわかります。
同様に、Dがゲームの最後だとすると、Dが40分本を読む時間がとれません。
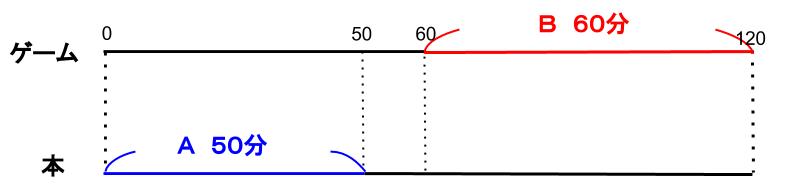
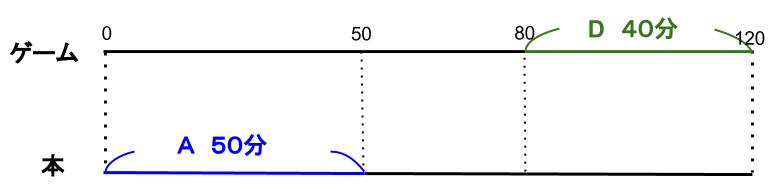
より、ゲームの最後はCと決まります。
次に、Cの直前にゲームをしたのがDだとすると、Dが40分本を読む時間がとれません。
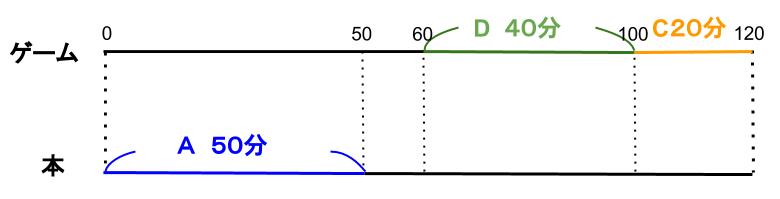
よって、Cの直前にゲームをしたのがB,ゲームをした順番は、DBCとなります。
すると、Bの本を読んだ順番が最後に決まります。CとDの本を読んだ順番は決まりません。
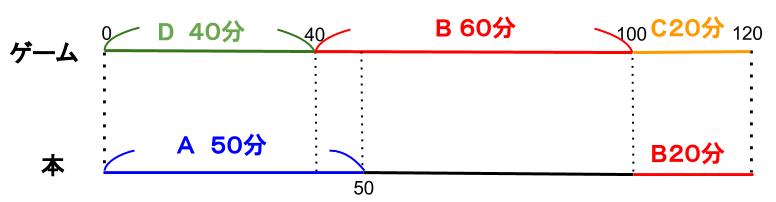
AとDが同時に絵を描いていた時間、BとCが休んでいます。
CとDがどの順番で本を読んだとしても、Cが本を読んでいたとき同時にBがゲームをしています。
Cが本を読んでいた時間は10分間です。
よって、BとCが同時に休んでいた時間は、10+20=30(分)です。
よって、AとDが同時に絵を描いていた時間も30分です。
スポンサーリンク
