基礎例題1
Aは朝8時に家を出発した。家から公園までは分速50mで歩き、公園から駅までは分速60mで歩いたところ、8時16分に駅に着いた。家から駅までの道のりは900mである。家から公園までの道のりは何mか。
解答
解説
速さの公式は覚えていますね?
速さ×時間=距離
です。
この式を変形することで、他の2つの式になります。
式変形をする手間を惜しまなければ、3公式を無理に覚える必要はありません。
速さの基本的な問題は、この公式で方程式をたてて解けば解決できます。
解法1 方程式
求めるものをXとおくのが常套手段ですね。
注 それ以外のものをXと置いた方が楽に解ける場合もあります。
家から公園までの距離をX(m)とすると、

なので、時間(=距離÷速さ)について立式すると、
X/50 + 900-X/60 =16
これを解いて、
X=300 求まりました。
解法2 方程式 未知数を時間にすると
家から公園まで歩いた時間をX(分)とし、距離(=速さ×時間)で立式すると、
50X + 60(16-X) =900
これを解いて、
X=6
よって、50×6=300
と求まりました。
こちらの方が計算が楽でしょうか。
解法1と大差ない気もします。
お好みでどうぞ。
基礎例題2
P地点からQ地点に向かって、AとBはバイクで、Cは歩いて同時にP地点を出発した。AはQ地点に着いてBを降ろすとただちに引き返し、歩いてきたCと出会うとCを乗せて再びQ地点に向かった。すると、AとCがQ地点に着いたのは、BがQ地点に着いてから48分後のことであった。このとき、PQ間の道のりは何kmか。ただし、バイクの速度は常に時速45km、Cの歩く速度は常に時速5km、人を降ろしたり乗せたりする時間はかからないものとする。
解答
解説
なんでもかんでも方程式!というのは上手ではありません。
登場人物の動きが複雑ですから、図で情報を整理してから、計算なり立式をしてきましょう。
1.スタートからBを降ろすまで(このときCがいる場所をR地点とします)
2.バイクが引き返してから、Cに出会うまで(出会った場所をS地点とします)
3.Cを乗せてQ地点に着くまで
この3段階にわけて図示したものが下図です。
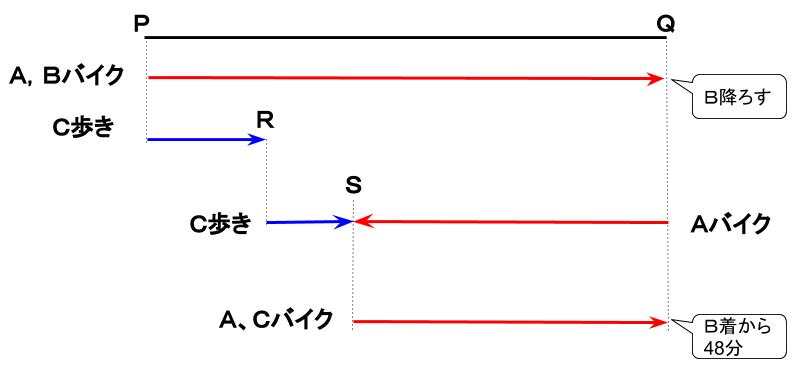
この図に、さらに情報を入れていきましょう。
BがQ地点に着いてから、A、CがQ地点に着くまでが48分なので、
QS間をバイクは24分で進んだことがわかります。
よって、バイクが24分で進む距離、歩いて24分で進む距離が計算できます。
バイクで24分 ⇒ 45 × 24/60=18(km)
歩いて24分 ⇒ 5 × 24/60=2(km)
よって、RQ間の距離は、18+2=20(km)です。
注 このRQ間の距離は、バイクとCが24分かけてお互いに向かい合って進んだ距離なので、
(45+5)× 24/60=20(km)
として求めることも多いです。旅人算と呼ばれています。
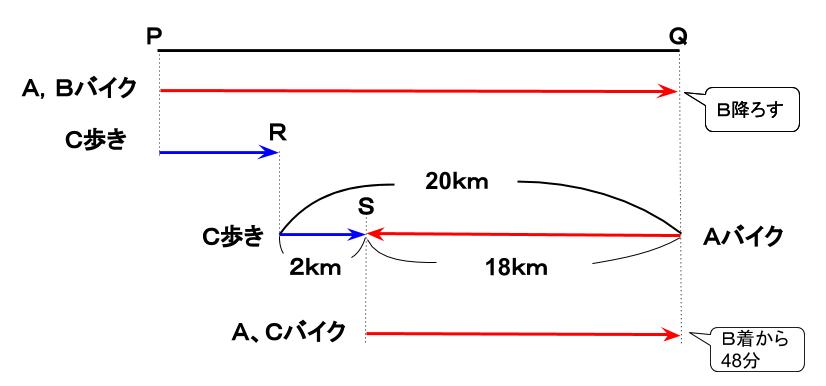
ここから先は、方程式、比、旅人算、いずれでも解けます。
解法1 方程式
PQ間の距離をX(km)とする。
PQ間をバイクで行く時間と、PR間を歩く時間は同じなので、
X/45 = X-20/5
これを解いて、
X=22.5
と求まります。
解法2 比の理用
速さの問題において、比の理用ができると非常に有利です。
PQ間をバイクで行く時間と、PR間を歩く時間は同じなので、
PQ:PR=45:5=9:1
となります。
式で確認すると以下のようになります。
速さ × 時間 =距離
45 × T =45T(PR)
5 × T =5T(PQ)
よって、下の図のようになります。
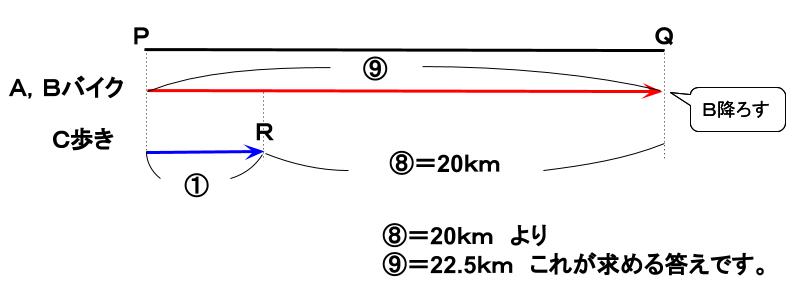
解法3 比の理用 別の視点
バイクとC(歩き)が、スタートから出会うまでを1つの区間として見ると
下図のようになります。
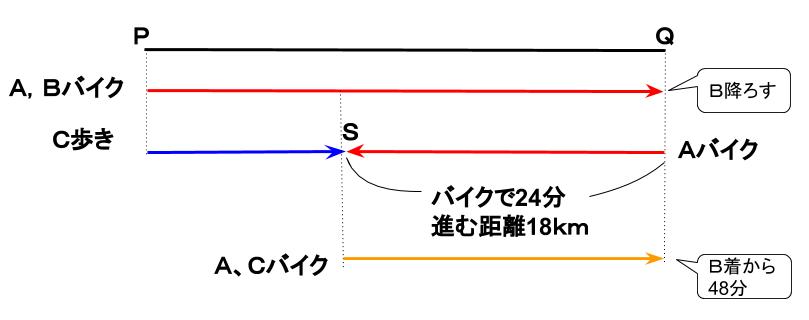
バイクとCが出会うまでに進んだ距離の比は速さの比と等しく、9:1です。
よって青矢印がXkmなら、赤矢印は9Xkm
赤矢印に相当する距離を、青矢印と18kmで表すと
9X=X+18×2
これを解いて、
X=4.5
求める距離は
X+18=22.5(km)
あるいは、
5X=22.5(km)
と求まりました。
スポンサーリンク
