基礎例題3
PQ間を結ぶ一本道を、P地点からはAが、Q地点からはBが互いに向かいあって同時に出発したところPQ間の5分の3地点で2人はすれ違った。その後AがQ地点に着き、その6分後にBがP地点に着いた。2人がすれ違ったのは出発から何分何秒後か求めなさい。
解答
解説
方程式ではなくて、比を活用する問題です。
AとBは同時に出発して、PQ間の5分の3地点ですれ違いました。
当然のことですがこの間、2人が歩いた時間は同じです。
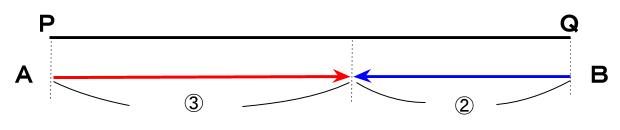
AとBが同じ時間に歩く距離の比は3:2です。
これは別の言い方をすると、AとBの速さの比が3:2である、になります。
式で確認すると以下のようになります。
速さ × 時間 = 距離
Aの速さ × 1 = 3
Bの速さ × 1 = 2
AとBの速さの比が3:2であることがわかります。
この2人が、PQ間という同じ距離をすすむと、かかる時間はどうなるのか。
同じ距離というのは1:1ということです。
速さ × 時間 = 距離
A 3 × ? = 1
B 2 × ? = 1
上の2つの積が等しいということは、
時間の比は2:3になります。
これを速さの比と時間の比が逆比になる、といいます。
速さ × 時間 = 距離
A 3 × ② = 1
B 2 × ③ = 1
2:3で、その差が6分なので
Aは12分
Bは18分
かけてPQ間を進んだことがわかります。
次にAに着目します。
Aは12分でPQ間を歩いたので、PQ間の5分の3地点まで進む時間は
12×3/5=7.2(分)=7分12秒です。
これはもちろんBに着目しても求まります。
Bは18分でQP間を歩いたので、QP間の5分の2地点まで進む時間は
18×2/5=7.2(分)=7分12秒です。
基礎例題4
AはP地点からQ地へ時速3kmで歩き、Q地点で3分休憩した後、時速4kmでP地点へ向かって引き返した。Bは、AがP地点を出発した15分後にQ地点を出発し、P地点へ向かって時速4kmで歩いた。そしてP地点に到着後、ただちに時速5kmでQ地点へ向かって引き返した。AとBがはじめてすれ違った地点をR、2回目にすれ違った地点をSとするとき、RS間の道のりは何kmか求めよ。ただし、PQ間の道のりは6kmとする。
解答
解説
登場人物の動きがかなり複雑です。
このようなときはダイヤグラムでまとめると楽に解けることが多いです。
注 ダイヤグラムは非常に強力な道具なので様々な問題で利用、練習してみることをおススメします。
それぞれにかかった時間は以下のようになります。
A 往路 6÷3=2時間=120分
A 復路 6÷4=1.5時間=90分
B 往路 6÷4=1.5時間=90分
B 復路 6÷5=1.2時間=72分
これらをダイヤグラムにまとめると以下のようになります。
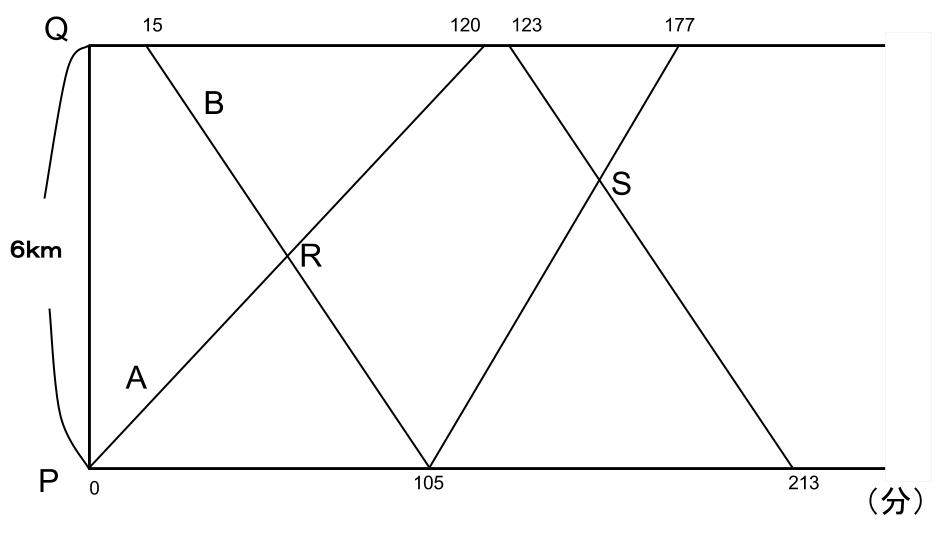
ダイヤグラムにおいて、交点は図形の問題として処理が可能です。
以下の色をつけた部分がそれぞれ相似になっています。
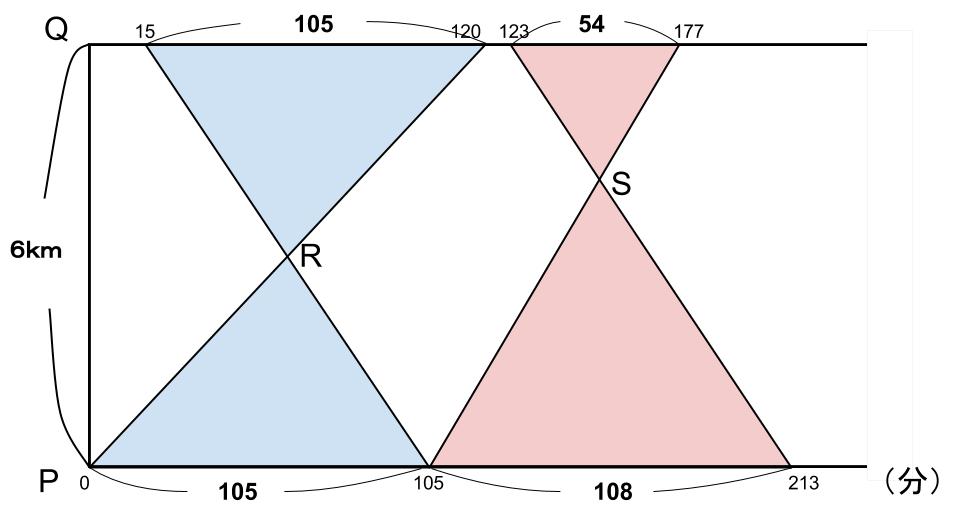
左の水色の三角形は、相似比が105:105=1:1
よって、R地点はPQ間を1:1に割った場所、中間地点です。つまりP地点から3kmです。
右のピンク色の三角形は、相似比が54:108=1:2
よって、S地点はPQ間を1:2に割った場所。つまりP地点から4kmです。
以上よりRS間の距離は、1kmと求まりました。
スポンサーリンク
