問題
5㎞離れた2地点A、B間を同じ経路で、兄はオートバイで、弟は自転車でそれぞれ走って一往復することになり、13時に弟が地点Aを出発した。その32分後に兄がA地点を出発し、地点Bの手前1㎞の地点で弟を追い越した。その後、復路を走る兄が弟とすれ違う時刻として正しいのはどれか。ただし、兄の速さは弟の速さの3倍であり、2人はそれぞれ一定の速さで走ったものとする。
- 13時44分
- 13時54分
- 14時04分
- 14時14分
- 14時24分
2011 東京都
解答と解説
解答
2
解説
兄が弟に追いついた地点をPとします。2人の速さの比が3:1なので、同じ距離を進むのにかかる時間の比は1:3です。その差2が32分なので、AP間にかかった時間は、兄は16分 弟が48分です。

これは、下のようなダイヤグラムにまとめられます。
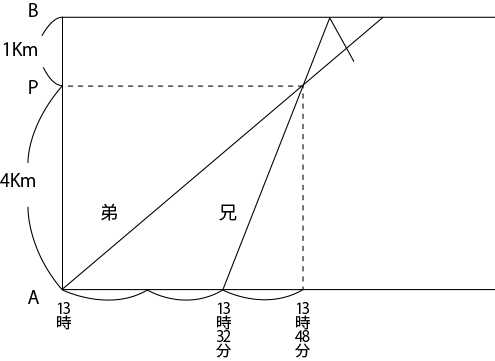
この後の解き方を2通り示します。
具体値で計算
兄の速さは、4000÷16=250(m/分) 弟の速さは兄の3分の1なので、250/3(m/分)
この2人がP地点を同時にスタートして、合計2km進むと出会うので、
2000÷(250+250/3)=6分
つまり2人はP地点を出発後6分で出会う。
13時48分の6分後なので、13時54分にすれ違うことがわかります。
グラフと比だけで処理も可能
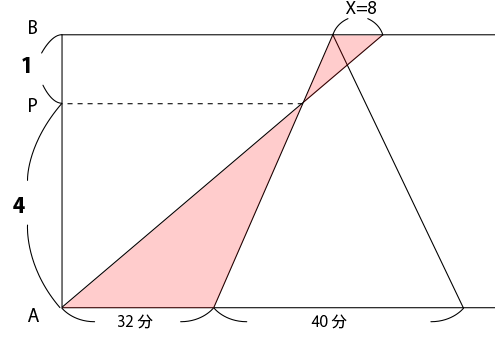
下図の赤色の部分の相似比は、1:4なので、X=8(分)と求まります。
また、兄がB到着後すぐに引き返してAに戻ることを考えます。
兄は4kmを16分かけて進む速さなので、AB間の往復10kmを40分かけて進みます。
次に下図の赤色の部分の相似比は、8:72=1:9 なので、2人がすれちがったのは、弟がAB間を進む途中、9/10の地点(4.5km)です。
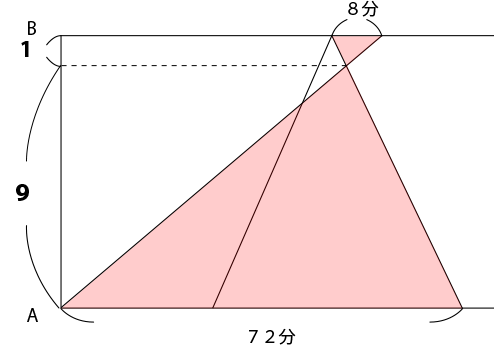
弟は4kmを48分かけて進みます。4.5km進むのにかかる時間は54分なので、求める時刻は13時54分です。
スポンサーリンク
