【不定方程式】基礎①

解答

解説

シュークリームを買った個数をＸ、チーズケーキを買った個数をＹとすると

120X + 280Y = 4480

Ｘ，Ｙの２つに未知数に対して式は1つなので、
この方程式の解は無限に存在します。

ただし、Ｘ、Ｙともに正の整数という制限があるので、この文章題の答えは有限個になります。
このような問題を、不定方程式の自然数解といいます。

では解いていきましょう。

120X + 280Y = 4480
このような不定方程式の解は、ずばり

「上手に見つける」

のです。
「あてはめて探す」
といってもいいでしょう。

ただし、闇雲に探しても大変ですから、
上手に見つけましょう。

以下、その見つけ方を詳しく紹介していきます。

まずは、数値を小さくして扱いやすくしましょう。
120X + 280Y = 4480
この式を40で割って、
３X ＋ ７Y ＝112
とします。
扱う数が小さくなればこの後の計算も楽ですし、カンで解が分かってしまうこともありますね。

さて、不定方程式の解の見つけ方、ですが、
X、Yの係数と、右辺の数に着目します。

今回は、112が７の倍数になっています。
３X ＋ ７Y ＝ 112
112÷７＝１６
よって、
3×０＋７×16 ＝112
つまり、X、Y＝（0,16)が見つかります。

X＝０は、文章題の答えとしては不適ですが、この不定方程式の解としてはOKです。
そして、1組解が求まれば、あとは芋づる式に見つかります。

なぜなら、Xを７増やし、Yを３減らすしかないからです。
（３と７の最小公倍数ずつずらすしか適するものがない）

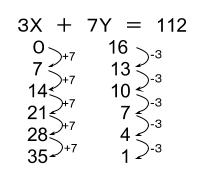
Xを7ずつ増やし、
Yを３ずつ減らします。

このように、不定方程式は解の組が１つ求まれば、他の解は容易に求められます。

この問題の答えは、シュークリームを買った個数（＝X）は何通りありうるか、
なので、
X＝７，１４、２１，２８，３５
の５通りです。

解答

解説

３X＋８Y＝８２
問題１のようにはなっていません。
８２は８でも３でも割り切れないからです。

しかし、８２と８に公約数があります。
２です。
つまり、８Yも８２も、２の倍数（偶数）になっています。
よって、３Xも偶数にならないといけません。

つまり、X＝２，４，６・・・と調べていくことで、あてはまる解を見つけることができます。
これで十分とも言えますが、さらに考察をすると、
８Yは4の倍数ですが、82は4の倍数ではありません。
よって、３Xが４の倍数ではいけません。

つまり、X＝２，６、１０、・・・と調べていくことで、あてはまる解を見つけることができます。
より、X＝６、Y＝８
を見つけます。
あとは芋づる式です。Xを8ずつ、Yを３ずつずらしていきます。

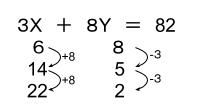
以上より、X,Y＝（６，８）（１４、５）（２２、２）の３組です。