【濃度 基礎】①

解答

解説

まずは
「食塩水の濃さ」
の定義から確認します（公式と呼ばれています）。

では解いていきましょう。

公式で計算

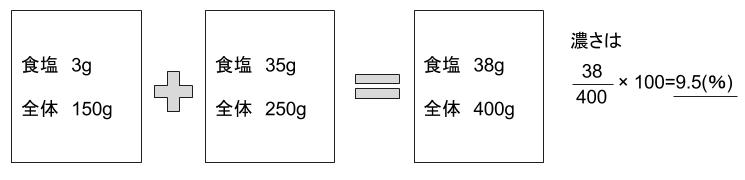
それぞれに溶けていた食塩の重さが計算できます。
150×0.02＝３
250×0.14＝35
よって、まぜた食塩水に溶けている食塩の重さは
３＋35＝38
まぜた食塩水の全体の重さは
150＋250＝400
よってその濃さは、38／400　×100　＝9.5（％）となります。

てんびん図

食塩水を混合する問題において、上記のような定義に従った計算とはべつに、
てんびん図という便利な道具があります。
これはてんびんのつり合いを求める問題と同一視する解法テクニックです。
詳しく紹介します。

問題再掲
濃さが２％の食塩水150gと濃さが14％の食塩水250gをまぜてできる食塩水の濃さは何か。

濃さは、てんびんの長さ、目盛りに相当します。
以下のような目盛りのついた棒をイメージします。

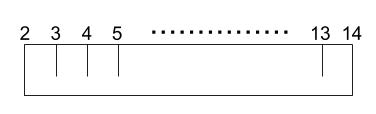
この棒のはしに重りをさげます。
２の下には150g
14の下には250gです。
これはもちろん、その濃さの食塩水の重さです。

そして、この棒はどこに糸をつければつりあうだろうか？
という問題になります。
つりあいの位置の目盛りが、混合後の濃度になります。

図は普通、以下のようにかきます。省略できるところは省略しましょう。

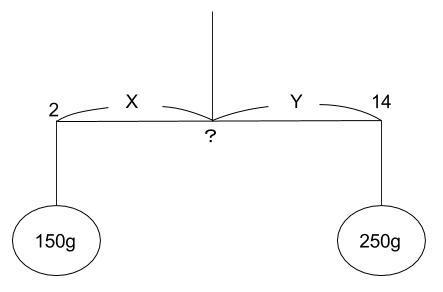
てんびんがつりあうのは、重さ×距離（支点までの）が等しくなるときなので、

150X＝250Y
となるときです。
X＋Y＝１２
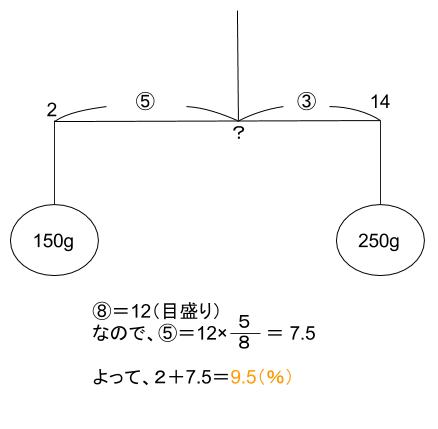
と合わせて、連立方程式を解けばXもYも求まりますが、

150X＝250Yのとき、
X：Y＝250：150＝5：3

のように、重さと長さが逆比になることを利用した方が計算は楽でしょう。

解答

解説

公式（方程式）で計算

はじめの食塩水に溶けていた食塩の重さは、
650×0.02＝13
求める量、追加した食塩の重さをXとすると以下のようになります。

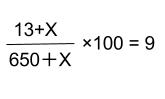
これを解いて、

X＝50
と求まります。

てんびん図

食塩は濃さ100％の食塩水とみなせます。これをてんびん図にすると以下のようになります。

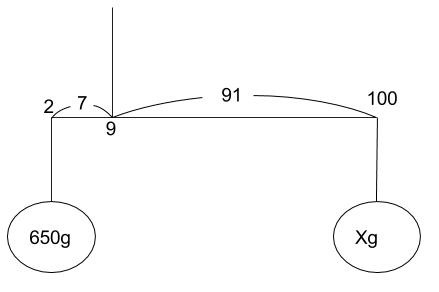
てんびんの釣りあいより、
91X＝７×650
X＝50

あるいは、長さの比が7：91＝1：13
より、重さの比は逆比の13：１になる。
650：X＝13：１
より、ｘ＝50