問題
ある作業をA、B、Cの3人で行う。1日に行う仕事量の割合が、A:B:C=3:3:2であり、3人が休まず仕事をすると30日で終了することが分かっている。今、作業の終了までにAが5日、Bが3日、Cが4日休むとき、この作業に要する日数はどれか。
- 33日
- 34日
- 35日
- 36日
- 37日
2011 特別区
解答と解説
解答
2
解説
3人の1日の仕事量を下のようにまとめる。
A 3X/日
B 3X/日
C 2X/日
全員が休まずに30日かけて終了する全仕事量は(3X+3X+2X)×30=240X です。
次に、3人の休んだ日をすべて最初に寄せて図示すると下のようになります。
3人一緒で仕事をした日をY日とします。
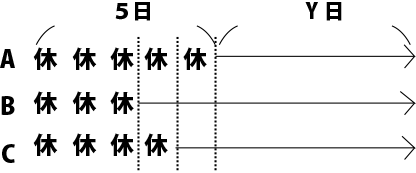
Bが2日、Cが1日、3人全員でY日の仕事をすると終了することがわかります。これを立式すると、
3X×2+2X×1+(3X+3X+2X)×Y=240X
これを解くと、Y=29(日)、よって全作業日数は、5+29=34(日)となります。
別解
※全員休まないで仕事をしたら・・・という視点でも解決できます。そのときの仕事量は全部で272X
272X÷(3X+3X+2X)=34(日)
スポンサーリンク
