基礎例題1
72とAの最小公倍数が648のとき、Aとして考えられる数は何個あるか。
解答
解説
最大公約数、最小公倍数の求め方の代表は連除法(はしご算)ですね。

P×Q=72なので、
P×Q×R=648 より
R=9
Qは72の約数で9と互いに素なので、
Q=1、2、4、8 の4通りが考えられます。

基礎例題2
135を割ると7余り、230を割ると6余る、正の整数がある。このような整数は何個あるか。
解答
解説
135を割ると7余る数とは、下図のxのような数です。
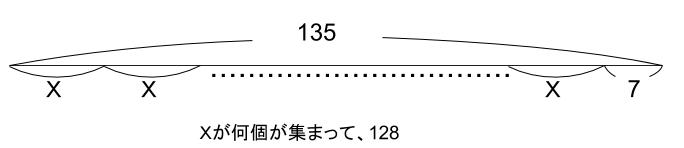
つまり、135を割ると7余る数とは、128の約数で、7より大きい数です。
7以下の数であるとき、あまりは6以下になるからです。
同様に
230を割ると6余る数とは、224の約数で、6より大きい数です。
以上2つを同時に満たす数は、128と224の公約数で、7より大きい数になります。
128と224の公約数は、128と224の最大公約数32の約数すべてなので、
32の約数を書き出します。
1、2、4、8、16、32
の6つが32の約数です。
該当するのは、8、16、32の3個になります。
基礎例題3
79、93、121の3つの数を、同じ数で割ったとき、あまりは等しくなりました。
割った数として考えられるものの総和はいくらか。
解答
解説
割った数をP、あまりをRとすると
79÷P=AあまりR・・・(Aは適当な整数)
と表せます。
この式を変形すると
79=PA+R
となります。
これは
Pで割ってRあまる数 ⇔ Pの倍数+R
ということです。しっかりと覚えておきましょう。
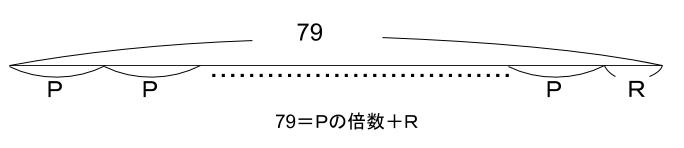
同様の表現でそろえると
79=Pの倍数+R・・・①
93=Pの倍数+R・・・②
121=Pの倍数+R・・・③
ここで各式の差をとります。
③-②より、28はPの倍数
②-①より、14はPの倍数
つまりPは28と14の公約数です。
より、Pは28と14の最大公約数である14の約数です。
14の約数は、1,2、7、14の4個。
ただし、1で割ってあまりがでることはないので、
P=2,7,14となります。
求める総和は2+7+14=23 となります。
参考
条件成立を自身の手で一度は確かめておきましょう。
2で割ったときのあまりはすべて1
7で割ったときのあまりはすべて2
14で割ったときのあまりはすべて9
スポンサーリンク
